Polynomial regression 多項式回帰
多項式回帰分析をRで実施する際に、polyを使用します。polyって何?とくにraw = TRUE って何?という点を調べたので、まとめておきます。
家賃のデータセットBostonを使いたいので、Bostonを含んだMASSパッケージをメモリにロードしておきます。
library(MASS)Bostonデータセットは、以下のような説明があります。medvが家賃で、lstatというのが変数です。家賃medvを、lstatで予想します。
Housing Values in Suburbs of Boston
lstat: lower status of the population (percent).
medv: median value of owner-occupied homes in \$1000s.
いきなり、単回帰分析を実施します。グラフ上に元データをプロットして、回帰分析による予想を線で表現します。
lm1 <- lm( medv ~ lstat, data = Boston )
tibble(x=lm1$model$lstat,
y=lm1$model$medv,
pred=lm1$fitted.values) %>%
ggplot() +
geom_point( aes(x=x,y=y,color=y) ) +
geom_line( aes(x=x, y=pred), size=1.2, color ="#636363" ) +
scale_colour_gradient( low="Blue", high="Pink" ) +
theme_minimal()+
theme(legend.position = 'none')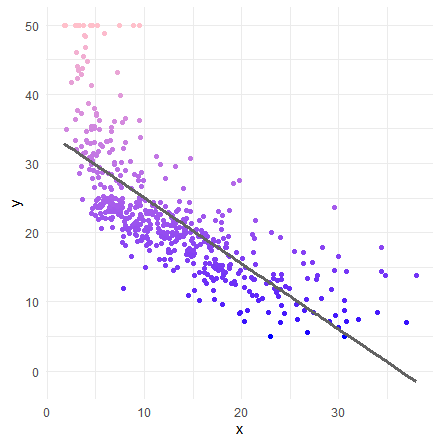
summary(lm1)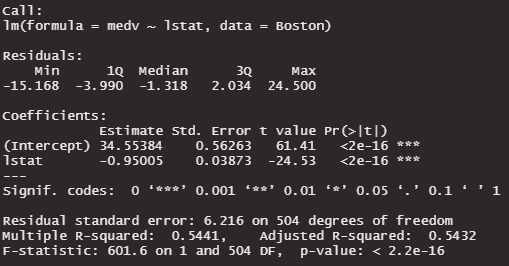
多項式回帰
本題の多項式回帰を実施します。変数の2乗を説明変数に追加します。2乗のところは大文字のiで始まるI()で囲みます。
lm2 <- lm( medv ~ lstat + I(lstat^2), data = Boston )
tibble(x=lm2$model$lstat,
y=lm2$model$medv,
pred=lm2$fitted.values) %>%
ggplot() +
geom_point( aes(x=x,y=y,color=y) ) +
geom_line( aes(x=x, y=pred), size=1.2, color ="#636363" ) +
scale_colour_gradient( low="Blue", high="Pink" ) +
theme_minimal() +
theme(legend.position = 'none')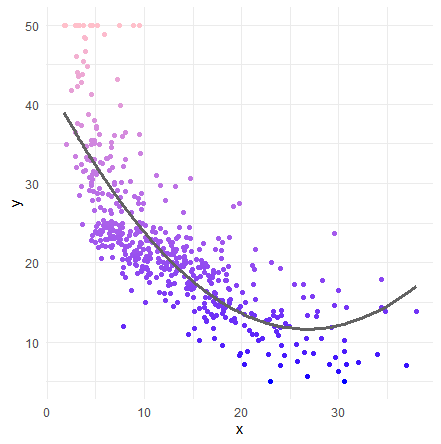
summary(lm2)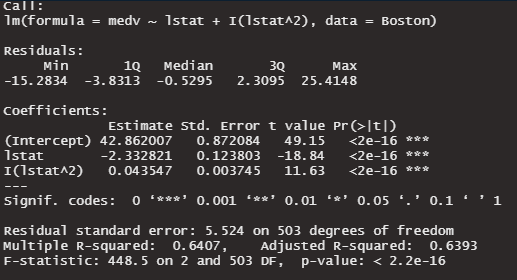
さきほどの単回帰のときと、多項式回帰(2乗)のR値を比較します。
単回帰分析:Adjusted R-squared 0.5432
多項式回帰(2乗):Adjusted R-squared 0.6393
式が複雑になるにつれ、学習データに対してフィットしていっています。過学習する副作用として、新しいデータを予測するのがダメになっていきます。
今度は、lstatの1乗、2乗、3乗の項を追加します。
lm3 <- lm( medv ~ lstat + I(lstat^2) + I(lstat^3), data = Boston )
tibble(x=lm3$model$lstat,
y=lm3$model$medv,
pred=lm3$fitted.values) %>%
ggplot() +
geom_point( aes(x=x,y=y,color=y) ) +
geom_line( aes(x=x, y=pred), size=1.2, color ="#636363" ) +
scale_colour_gradient( low="Blue", high="Pink" ) +
theme_minimal()+
theme(legend.position = 'none')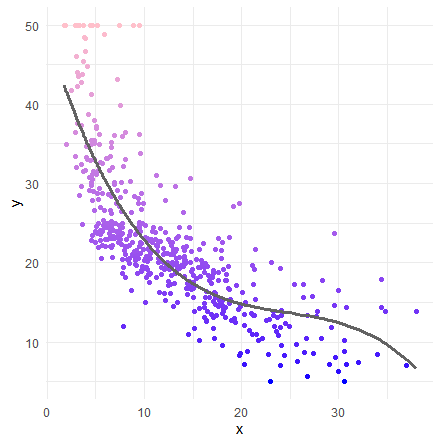
summary(lm3)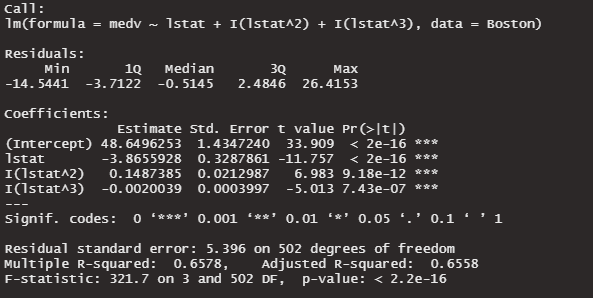
さらにR値が上昇しました!
今まで、手動でIを使って多項式を書いていましたが、自動で多項式を生成する方法があります。polyです。さきほどの以下の式を再掲します。これをpolyで書き直したいと思います。
lm3 <- lm( medv ~ lstat + I(lstat^2) + I(lstat^3), data = Boston )これは、以下のように書き換えることができます。poly(変数, degree = 何乗するか。ここでは3。, raw = TRUE)。
lm3_poly <- lm( medv ~ poly(lstat, degree = 3, raw=TRUE), data = Boston )raw = TRUEってなんでしょうか。?polyで調べると、raw – if true, use raw and not orthogonal polynomials.と書かれています。、、、意味がわかりません。
とりあえず、実験してみます。1:5の配列を使って、raw=TRUEのFALSEを比べてみます。まずはTRUEで。
poly_raw <- poly(x <- 1:5, degree = 3, raw=TRUE)
poly_raw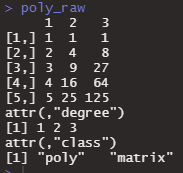
これは予想通りですね。raw = FALSEにしてみます。
poly_ortho <- poly(1:5, degree = 3, raw=FALSE)
poly_ortho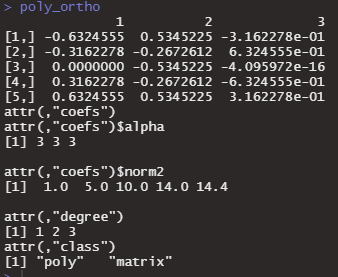
なんでしょうかこれは。Stack overflowで調べてみます。
・What does the R function `poly` really do?
・poly() in lm(): difference between raw vs. orthogonal
どうやら、falseの場合はただ単に、〇乗を返してくれるだけではないようです。まずは〇乗して、スケーリングを実施して、その後直交行列を返してくれるようです。なぜ、このような計算が必要なのでしょうか?理由としては、2つ提案されています。
1 ある数字の2乗、3乗を変数にすると、それらがcorrelationを強く持ち、multicollinearityを起こしてしまう。そのため、変数たちがmulticollinearityを起こさないために直交化させる必要がある。
2 直交化しない場合には、例えば2乗の項までで回帰分析したときに得られた変数の係数と、それに3乗の項を追加して解析したときに得られる変数の係数が大きく変わってしまいます。直交化することで、係数が大きく変わることを防ぐことができるそうです。
multicollinearityのところは腑に落ちましたが、2のメリットはなんなのかよくわからないです。
とりあえず、polyで生成された配列が直交するかどうかを確かめてみたいと思います。行列の掛け算は%*%です。まずは、raw = TRUEで直交しないやつです。
poly_raw <- poly(x <- 1:5, degree = 3, raw=TRUE)
poly_raw[,1] %*% poly_raw[,2]
poly_raw[,2] %*% poly_raw[,3]
poly_raw[,1] %*% poly_raw[,3]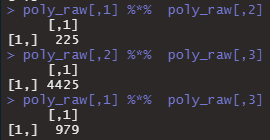
今度は、raw = FALSEで直交しているやつです。行列の掛け算をすると0になると思われます。
poly_ortho <- poly(1:5, degree = 3, raw=FALSE)
poly_ortho[,1] %*% poly_ortho[,2]
poly_ortho[,2] %*% poly_ortho[,3]
poly_ortho[,1] %*% poly_ortho[,3]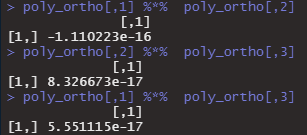
ほぼ0ですね。なんとなくわかってきた気がしました。ところで、polyはどんな計算を実施しているのでしょうか。polyに関して唯一日本語で解説してくださっているサイトを見つけました。西陣に住むデータ分析屋のブログ。このサイトでは、パッケージ内部まで覗いて研究なさったらしく、2項の場合の計算方法まで教えてくれています。
第一項
x <- 1:5
b1 <- (x - mean(x)) / sqrt(sum((x - mean(x))^2))これが、さっきのpoly_ortho <- poly(1:5, degree = 3, raw=FALSE)の1項目と同じか確かめます。
all.equal(poly_ortho[,1],b1)TRUE おお!!
第2項
x <- 1:5
b2a <- x^2 - b1 * sum(x^2 * b1)/sum(b1^2)
b2 <- (b2a - mean(b2a)) / sqrt(sum((b2a - mean(b2a))^2))
all.equal(poly_ortho[,2],b2)TRUE
おお!!理解しました。待って。書かれていない第3項は? 第2項のアナロジーで計算してみます。
b3a <- x^2 - b2 * sum(x^2 * b2)/sum(b2^2)
b3 <- (b3a - mean(b3a)) / sqrt(sum((b3a - mean(b3a))^2))
all.equal(poly_ortho[,3],b3)“Mean relative difference: 1.333333”
違った。。もういい。計算方法はおいといて、計算された後の配列は直交しているのは確認できたので次に進みます。
さきほど、手動で3乗の非直交多項式回帰分析をしました。今度は、polyを使って、直交で(raw=FALSE)やってみたいと思います。
lm3_poly_ortho <- lm( medv ~ poly(lstat, degree = 3, raw = FALSE), data = Boston )
tibble(x=Boston$lstat,
y=lm3_poly_ortho$model$medv,
pred=lm3_poly_ortho$fitted.values) %>%
ggplot() +
geom_point( aes(x=x,y=y,color=y) ) +
geom_line( aes(x=x, y=pred), size=1.2, color ="#636363" ) +
scale_colour_gradient( low="Blue", high="Pink" ) +
theme_minimal() +
theme(legend.position = 'none')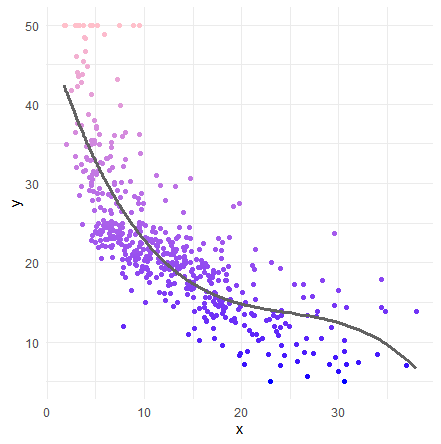
あれ、さっきと全然変わらない気がする。raw = FALSE 直交と、row = TRUE 非直交で比較してみよう。
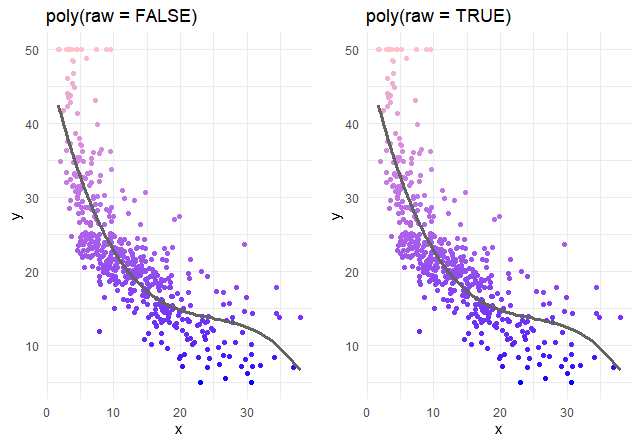
グラフ上は同じに見えます。中身を見てみます。
summary(lm3_poly_ortho)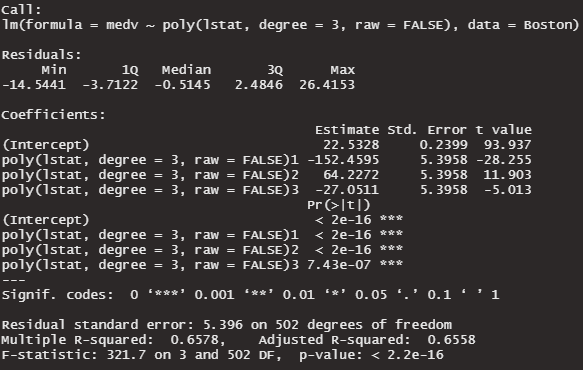
Adusted R-squaredの数値が全く一緒。変わったのは、係数と係数のp値のみ。
直交の良さがでていない気がします。1乗、2乗、3乗の3つの変数だけだとmulticollinearityの影響が少ないのかもしれません。10乗くらいでやってみます。
lm10_poly <- lm(medv ~ poly(lstat, degree = 10, raw = TRUE), data = Boston )
lm10_poly_ortho <- lm(medv ~ poly(lstat, degree = 10, raw = FALSE), data = Boston )
summary(lm10_poly)
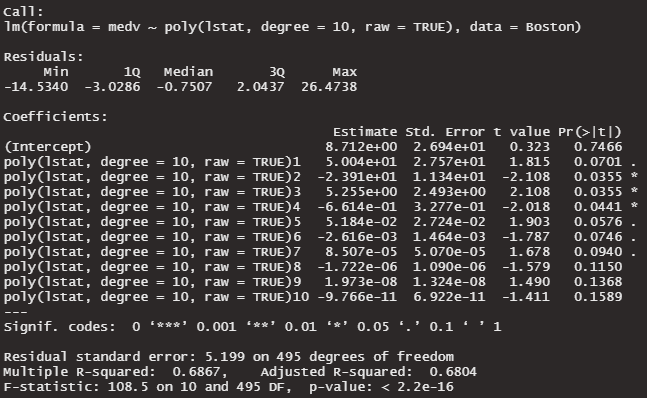
summary(lm10_poly_ortho)非直交 raw = TRUE
多くの係数が、p > 0.05になっています。係数が0である可能性を否定できません。multicollinearityの影響がでてきました。有意水準5%で、0ではない係数は3つだけです。
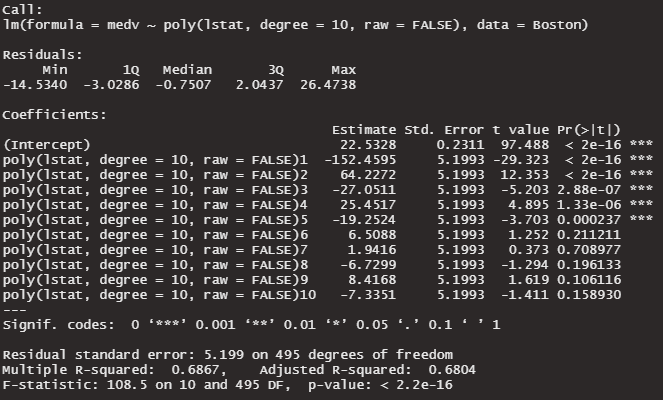
直交 raw = FALSE
有意水準5%で、0ではない係数は6つになりました。3つ多くなりました。ただ、Adjusted R-Suqredは変化ありませんでした。
ところで、マルチコの検査をしてみたいと思います。
multicollinearityの診断は、VIFという指標で行います。carというパッケージで実施できます。使い方は、vif( lm( )で作ったモデル ) です。
library(car)
lm10_poly <- lm(medv ~ poly(lstat, degree = 10, raw = TRUE), data = Boston )
vif(lm10_poly)エラーがでてしまいました。
vif.default(lm10_poly) でエラー: model contains fewer than 2 terms
どうやらめんどうですが、polyを分解してdataframeを作り直す必要がありそうです。力尽きました。
次回の記事で確認します。
