Global MoranとLocal Moran
をつかって死亡率に地域集積性があるか検定する。
地域集積性のデータの種類によって集積性の検定は異なる。自分の今の理解だと以下の整理。
| 種類 | 検定の名前 |
|---|---|
| ポイントデータの存在を用いた集積性の検定 | Ripley’s K/L |
| ポイントデータの連続変数を用いた集積性の検定 | Moran |
| ポリゴンの連続変数を用いた集積性の検定 | Moran, kulldorff |
GISの検定系はpythonよりもRのほうが充実。しかしながらpythonで実装。kulldorffのクラスター検定までやろうとするとRしかできない。
使うライブラリは、libpysal esda geopandas。
まずはライブラリの説明から
元々、PySALというライブラリがあったが、巨大になりすぎたため、機能ごとに分割され、その基盤部分がlibpysalとして、統計の一部がesdaとして独立した。
libpysal = library + PySAL
PySALはもともと Python Spatial Analysis Library の略。
esda = Exploratory Spatial Data Analysisの頭文字。
空間統計学の分野では 昔からESDA という用語が定着しているらしい。
サンプルのデータセットを使ってやってみる。
import libpysal
a = libpysal.examples.available()
a
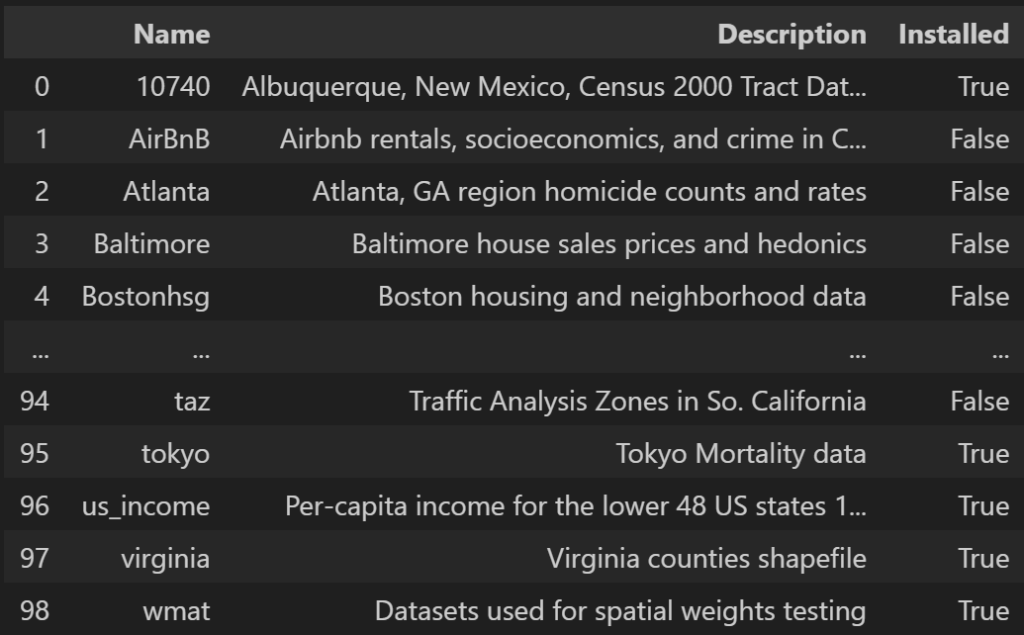
Tokyoというのがあるので詳しく見てみる。
data = libpysal.examples.load_example("tokyo")
data.explain()
Tokyo Mortality data ——————–
* Tokyomortality.csv: Attribute data (n=262, k=9)
* Readme_tokyomortality.txt: Metadata
* tokyomet262.shp: Polygon shapefile (n=262)
Source: Nakaya T, Fotheringham A, Brunsdon C, Charlton M. Geographically weighted poisson regression for disease association mapping. Statistics in Medicine. 2005;24(17):2695–2717. https://doi.org/10.1002/sim.2129
東京の死亡率のデータのようです。
data.get_file_list()でダウンロードされたファイルパスが見れる。
ファイルの説明が欲しいので、以下のファイルを見る。
with open(data.get_path("Readme_tokyomortality.txt"),"r") as f:
a = f.read()
print(a)
Fields
IDnum0: sequential areal id
X_CENTROID: x coordinate of areal centroid
Y_CENTROID: y coordinate of areal centroid
db2564: observed number of working age (25-64 yrs) deaths
eb2564: expected number of working age (25-64 yrs) deaths
OCC_TEC: proportion of professional workers
OWNH: proportion of owned houses
POP65: proportion of elderly people (equal to or older than 65)
UNEMP: unemployment rate
また、Note 1: IDnum0 in tokyomortality.txt can be matched with AreaID in this shapefile. と書いてある。
使うファイルは、shpファイルと、attributeのファイルの2つということが分かり、2つのファイルのリンクは、IDnum0とAreaIDという列。
shapeファイルを読み込む
import geopandas as gpd
gdf = gpd.read_file(data.get_path("tokyomet262.shp"))
gdf

attributeのファイルを読み込む。そして、標準化死亡比(SMR: Standardized Mortality Ratio)を計算する(観測死亡数/年齢構成などを補正した期待死亡数)
import pandas as pd
attribute = pd.read_csv(data.get_path("Tokyomortality.csv"))
attribute["StandardizedMortalityRatio"] = attribute["db2564"]/attribute["eb2564"]
attribute

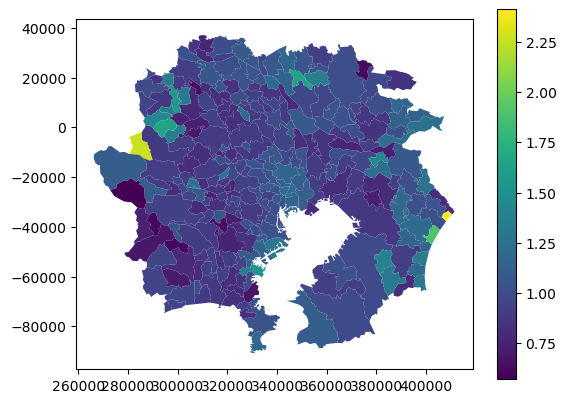
上記2つを結合して可視化。
gdf_attributed = pd.merge(gdf,attribute,left_on="AreaID",right_on="IDnum0",how="left")
gdf_attributed.plot(column = "StandardizedMortalityRatio",legend=True)
説明(by chatGPT)
# Global Moran’s I を直感でつかむ
## 一言でいうと
「似た値どうしが空間的に集まっているか」を測る指標。
– 似た値が近くに集まる → 正の値(+)
– 似た値がバラバラに散らばる → 0 に近い
– 近い場所ほど逆の値(高い所の隣が低いなど) → 負の値(−)
# 直感的な分解:Moran’s I の3つの要素
Global Moran’s I は、ざっくり言うと次の3つの要素の掛け合わせです。
## ① 「値の偏差 × 空間的な近さ」
– 各地点の値が平均からどれだけズレているか(偏差)
– その地点と他の地点がどれだけ近いか(空間重み)
これを全部の組み合わせで足し合わせる。
近くにある地点どうしの偏差が同じ符号ならプラスに働く。
逆符号ならマイナスに働く。
## ② 「全体のバラつきで割る」
偏差の総量(分散)で割ることで、
“空間的な偏りがどれだけ強いか”を標準化している。
## ③ 「重みの総量で調整」
空間重み(近さ)の合計で割ることで、
地域数や重みのスケールに依存しない指標にしている。
# もっと直感的なイメージ:重り付きのシーソー
次のように考えると一気に理解が進む。
### ● 各地点の「偏差」は重りの大きさ
### ● 空間的な近さは「てこの距離」
### ● 似た偏差の地点が近くにあると、同じ方向に力がかかる
→ シーソーが大きく傾く(Moran’s I が大きくなる)
### ● 逆の偏差の地点が近くにあると、反対方向の力がかかる
→ シーソーが逆向きに傾く(Moran’s I が負になる)
### ● 偏差がランダムに散らばっていると
→ 力が相殺されて傾かない(Moran’s I ≈ 0)
# 計算式を“意味”で読むとこうなる
$$
I = \frac{N}{W} \cdot \frac{\sum_{i}\sum_{j} w_{ij}(x_i – \bar{x})(x_j – \bar{x})}{\sum_i (x_i – \bar{x})^2}
$$
これを直感で読むと:
– 分子:
“近い地点どうしの偏差の掛け算を全部足したもの”
→ 空間的な似た者同士の集まり具合
– 分母:
“全体のバラつき”
→ そもそもデータがどれだけ散らばっているか
– N/W:
“スケール調整”
→ 地域数や重みの合計に依存しないようにする
# 直感的な例
## 例1:高い値が北側に固まっている
→ 近い地点どうしの偏差が同じ符号
→ 掛け算はプラス
→ Moran’s I は正
## 例2:高い値の隣に低い値が並ぶチェッカーパターン
→ 近い地点どうしの偏差が逆符号
→ 掛け算はマイナス
→ Moran’s I は負
## 例3:値がランダムに散らばる
→ プラスとマイナスが相殺
→ Moran’s I ≈ 0
# ローカルモラン(Local Moran’s I)の直感的な理解
Global Moran’s I が「全体として空間的自己相関があるか」を測るのに対して、
Local Moran’s I は “どの地点がその自己相関を生み出しているのか” を特定する指標です。
# 一言でいうと
「この地点は周囲と比べてどれくらい“似ている”か、または“浮いている”か」を測る指標。
– 周囲と似た値 → クラスター(集積)
– 周囲と逆の値 → アウトライヤー(異常点)
# Local Moran’s I が測っているもの
## ① その地点の偏差(平均からのズレ)
$$
(x_i – \bar{x})
$$
## ② 周囲の地点の偏差の平均(空間的ラグ)
$$
\sum_j w_{ij}(x_j – \bar{x})
$$
## ③ この2つの掛け算
$$
I_i = (x_i – \bar{x}) \cdot \sum_j w_{ij}(x_j – \bar{x})
$$
“自分の偏差 × 周囲の偏差” が Local Moran の本質
# 直感的な読み方
## ● 自分も周囲も高い(High–High)
→ 正 × 正 → 正の値(クラスター)
## ● 自分も周囲も低い(Low–Low)
→ 負 × 負 → 正の値(クラスター)
## ● 自分は高いが周囲は低い(High–Low)
→ 正 × 負 → 負の値(アウトライヤー)
## ● 自分は低いが周囲は高い(Low–High)
→ 負 × 正 → 負の値(アウトライヤー)
# もっと直感的なイメージ:磁石のような振る舞い
– 各地点は「プラス(高い)」か「マイナス(低い)」の磁石を持っている
– 近くの磁石と同じ極なら引き合う → クラスター
– 逆の極なら反発する → アウトライヤー
Local Moran’s I は、
「この地点は周囲と引き合っているか、反発しているか」
を数値化している。
# 🗺️ Local Moran が教えてくれる4つのパターン
| パターン | 意味 |
|———|——|
| **High–High** | 高い値が高い値に囲まれる → ホットスポット |
| **Low–Low** | 低い値が低い値に囲まれる → コールドスポット |
| **High–Low** | 高い値が低い値に囲まれる → 高値の異常点 |
| **Low–High** | 低い値が高い値に囲まれる → 低値の異常点 |
Global と Local の違いを一言で
– Global Moran’s I
→ 全体として“まとまり”があるか
– Local Moran’s I
→ どの地点がその“まとまり”を作っているか
→ どの地点が“浮いている”か
直感的な例
例:東京の家賃データ
– 新宿・渋谷・港区あたりが High–High
– 多摩地域の一部が Low–Low
– 高級住宅地の中に突然安い物件があれば Low–High
– 郊外の中に突然高い物件があれば High–Low
Moranを計算するためには、空間重みが必要。
from libpysal.weights import Queen
weights = Queen.from_dataframe(gdf_attributed)
weights.neighbors
{0: [8, 17, 18, 11],
1: [102, 103, 24, 25, 107],
2: [30, 7],
3: [8, 21],
4: [20, 118, 6, 8, 29],
weights.weights
{0: [1.0, 1.0, 1.0, 1.0],
1: [1.0, 1.0, 1.0, 1.0, 1.0],
2: [1.0, 1.0],
3: [1.0, 1.0],
4: [1.0, 1.0, 1.0, 1.0, 1.0],
weights.transform = "r"
weights.weights
{0: [0.25, 0.25, 0.25, 0.25],
1: [0.2, 0.2, 0.2, 0.2, 0.2],
2: [0.5, 0.5],
3: [0.5, 0.5],
4: [0.2, 0.2, 0.2, 0.2, 0.2],
空間重みの説明(by chatGPT)
# **PySAL における Weights(空間重み)の考え方**
PySAL(libpysal)は、空間重みを地理的な隣接関係」または「距離」から自動生成する仕組みを持っています。
大きく分けて次の2系統。
1. 隣接ベース(Contiguity-based)
– Queen(接点共有)
– Rook(辺共有)
2. 距離ベース(Distance-based)
– k-Nearest Neighbors
– 距離閾値(threshold distance)
– 距離の逆数などの連続重み
# 1. 隣接ベースの Weights の計算方法
## Queen 隣接(接点共有)
“`python
from libpysal.weights import Queen
w = Queen.from_dataframe(gdf)
“`
### 仕組み(内部で何をしているか)
– 各ポリゴンの境界(edges)と頂点(vertices)を解析
– 1点でも接していれば隣接とみなす
– 隣接していれば `w[i][j] = 1`、そうでなければ 0
– 最後に `w.transform = “r”` で行標準化(各行の合計が1になる)
## Rook 隣接(辺共有)
“`python
from libpysal.weights import Rook
w = Rook.from_dataframe(gdf)
“`
### 仕組み
– 辺を共有している場合のみ隣接
– Queen より厳しい隣接条件
—
# 2. 距離ベースの Weights の計算方法
## k-Nearest Neighbors(kNN)
“`python
from libpysal.weights import KNN
w = KNN.from_dataframe(gdf, k=4)
“`
### 仕組み
– 各地点の重心(centroid)を計算
– 距離を測り、最も近い k 個を隣接とする
– `w[i][j] = 1`(隣接)
– `transform=”r”` で標準化可能
—
## 距離閾値(threshold distance)
“`python
from libpysal.weights import DistanceBand
w = DistanceBand.from_dataframe(gdf, threshold=5000) # 5km以内
“`
### 仕組み
– 各地点の重心間距離を計算
– 閾値以下なら隣接
– `binary=True` なら 1/0
– `binary=False` なら距離の逆数などの連続重みも可能
—
# Weights の中身を確認する方法
## 隣接リスト(辞書形式)
“`python
w.neighbors
“`
例:
“`python
{0: [1, 2, 5], 1: [0, 3], …}
“`
## 重み値
“`python
w.weights
“`
例:
“`python
{0: [0.33, 0.33, 0.33], …}
“`
## 行列形式に変換
“`python
w.full()[0] # numpy 行列
“`
# PySAL が Weights を計算する流れ(内部ロジック)
1. ジオメトリの読み込み
– ポリゴンなら境界と頂点
– 点なら座標
2. 隣接判定 or 距離計算
– Queen/Rook → トポロジー解析
– KNN → 距離行列を作成し k 個選択
– DistanceBand → 閾値以下を選択
3. 重みの付与
– デフォルトは binary(1/0)
– 距離ベースなら距離の逆数なども可能
4. 標準化(transform)
– `”r”`:行標準化(最も一般的)
– `”b”`:binary のまま
– `”v”`:分散安定化
– `”d”`:距離の逆数
# 標準化とは何をしているのか
「各地点の重みの合計が 1 になるように調整すること」
これが最も一般的な 行標準化(row-standardization) です。
PySAL では `w.transform = “r”` と書くとこれが適用されます。
# なぜ標準化が必要なのか
## ① 隣接数の違いを公平にするため
– 都心のように隣接が多い地域
– 郊外のように隣接が少ない地域
このままでは、隣接が多い地域の方が Moran’s I の計算で 不当に大きな影響力を持ってしまう。
行標準化すると:
– 隣接が 3 個 → 各重みは 1/3
– 隣接が 8 個 → 各重みは 1/8
どの地点も「周囲から受ける影響の総量」が同じになる
## ② Moran’s I の値がスケールに依存しなくなる
標準化しないと、
– 地域数
– 隣接の密度
– 距離のスケール
などによって Moran’s I の値が変わってしまう。
標準化すると、
**「空間的自己相関の強さ」だけが純粋に測れる**。
## ③ Local Moran の解釈が安定する
Local Moran’s I は
(x_i – \bar{x}) \times \sum_j w_{ij}(x_j – \bar{x})
で計算されるので、
重みの合計が地点によって違うと **比較ができなくなる**。
行標準化すると、
「周囲の平均的な偏差」を見る形になり、
クラスター(HH, LL)やアウトライヤー(HL, LH)が安定して判定できる。
# 標準化の種類(PySAL の transform)
| transform | 意味 | 使いどころ |
|———-|——|————-|
| `”r”` | 行標準化(Row-standardized) | Moran’s I の標準的な設定 |
| `”b”` | Binary(1/0 のまま) | 重みの強さを変えたくない場合 |
| `”v”` | Variance-stabilizing | 特殊用途 |
| `”d”` | 距離の逆数などの連続重み | 距離ベースの解析 |
最もよく使われるのは “r”(行標準化)。
# 直感的なイメージ:重りの総量を揃える
各地点は「周囲から受ける影響の総量」を持っていると考えるとわかりやすい。
– 標準化なし
→ 隣接が多い地点は重りが大きく、計算に強く効く
– 行標準化
→ 隣接が多くても少なくても、合計は常に 1
つまり、
「どの地点も同じだけ周囲から影響を受ける」
という公平な状態になる。
Global Moranを計算する
from esda import Moran
moran = Moran(y=gdf_attributed["StandardizedMortalityRatio"] , w=weights)
print("Global Moran's I:", moran.I)
print("p-value:", moran.p_sim)
Global Moran's I: 0.19397271713412056
p-value: 0.001
もう一回やると、p-valueが異なる。シュミレーションのバリエーションのようだ。import numpy as np; np.random.seed(42)で固定しておけば、一定の答えが出てくる。
p値が0.05以下なので、優位水準0.05で優位。地域集積性あり
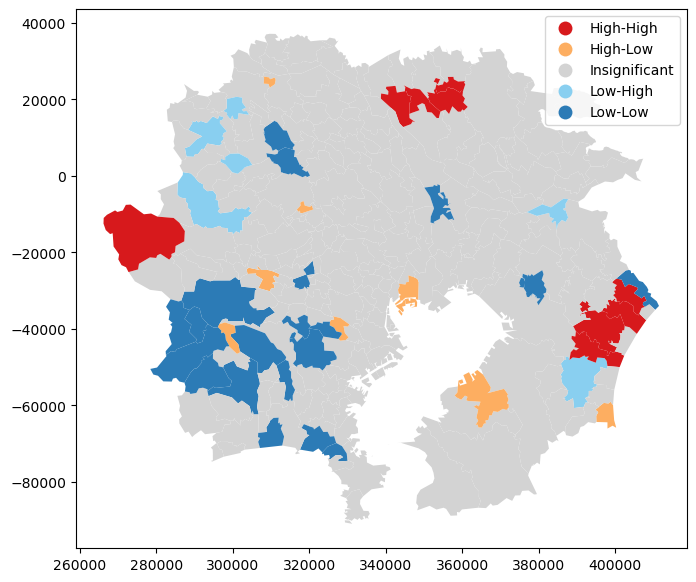
Local Moran
from esda import Moran_Local
import matplotlib.pyplot as plt
local_moran = Moran_Local(y=gdf_attributed["StandardizedMortalityRatio"], w=weights)
fig, ax = plt.subplots(1, 1, figsize=(10, 7))
local_moran.plot(gdf=gdf_attributed, legend=True, ax=ax)
plt.show()
local_moran.plot_combination(gdf=gdf_attributed,attribute=gdf_attributed["StandardizedMortalityRatio"])
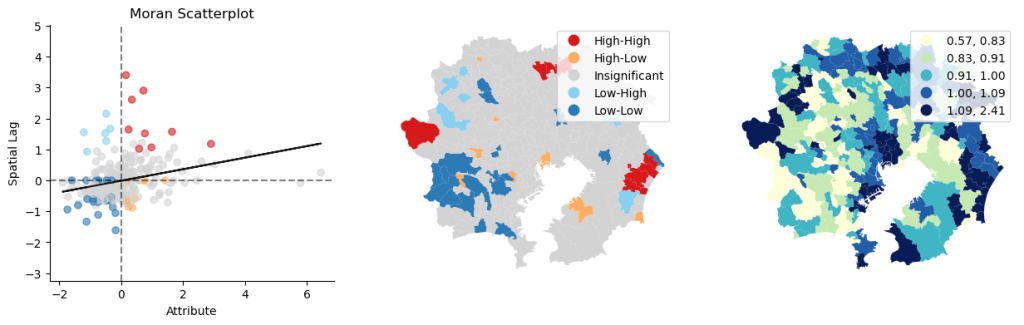
詳しく見たい
gdf_attributed["type"] = local_moran.q
gdf_attributed["significant"] = local_moran.p_sim < 0.05
gdf_attributed["type"].unique()
array([3, 2, 4, 1])
現在は、high-highのようなパターンが数字で表現されているので、わかりやすいように変換。
def convert_meaning(x):
match x:
case 1: return "High-High"
case 2: return "Low-Low"
case 3: return "High-Low"
case 4: return "Low-High"
case _: raise ValueError()
gdf_attributed["type"] = gdf_attributed["type"].apply(convert_meaning)
gdf_attributed.head()
死亡率がhigh-highで空間相関がある地域。
(gdf_attributed
.query("significant == True")
.query("type == 'High-High'")
.filter(["AREANAME","StandardizedMortalityRatio"])
)
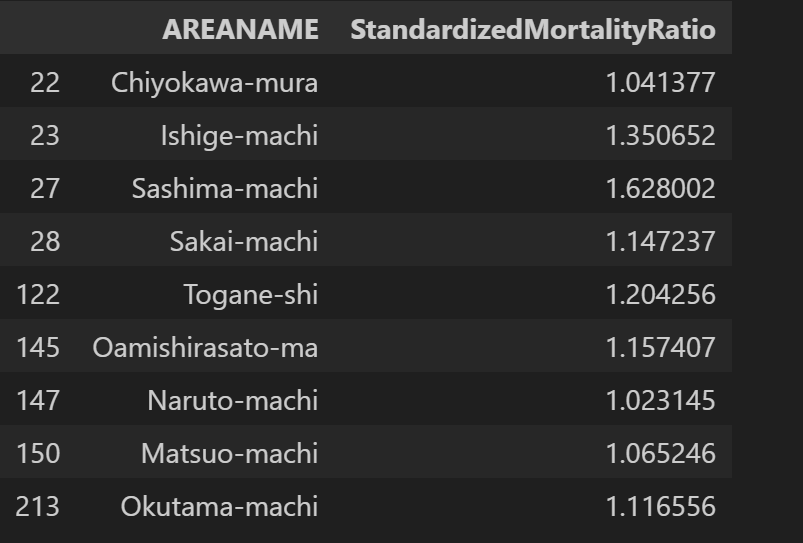
茨城と千葉?
今度は死亡率がlow-lowの空間相関がある地域
(gdf_attributed
.query("significant == True")
.query("type == 'Low-Low'")
.filter(["AREANAME","StandardizedMortalityRatio"])
)
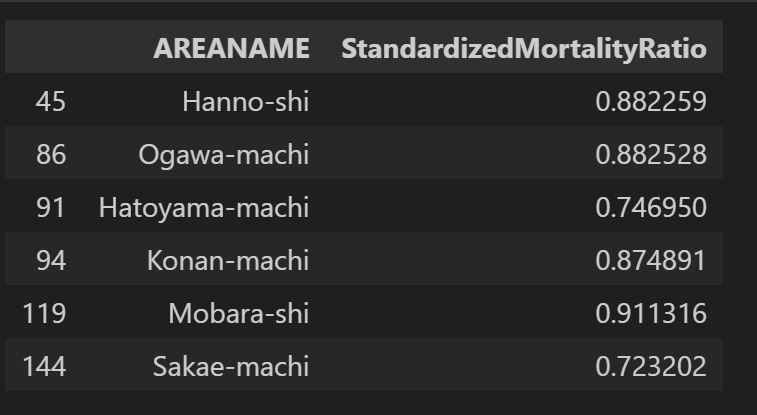
埼玉と千葉?
ポイントデータはこちらの記事にて
