重回帰分析において、多重共線性multicollinearityによりうまく予想できないことがあります。multicollinearityは、変数同士が似た動きをすると起こります。例えば、変数1と変数2に強い相関があるとき等です。
multicollinearityの診断に、VIF(variance inflation factor)が使われます。それぞれの変数ごとにVIFが計算され、VIFが5以上の変数は除くべきとされています。
以下の記事と同様にbostonデータセットを使って、多項式回帰分析を実施し、その変数についてmulticollinearityの診断をします。
家賃のデータセットBostonを使いたいので、Bostonを含んだMASSパッケージをメモリにロードしておきます。家賃medvを、lstatという名の変数で予想します。
raw = TRUEを付けた場合の変数
lstat^1, lstat^2, lstat^3, ・・・ , lstat^10
これは、変数lstatの動きが、すべての変数の動きを決めているので、multicollinearityの影響を受けてしまいます。
raw = FALSEを付けた場合の変数
f1(lstat^1), f2(lstat^2), f3(lstat^3), ・・・ , f10(lstat^10)
これらの変数が直交しています。直交することで単純な多項式でのmulticollinearityの影響を排除することができます。
library(MASS)
lm10_poly <- lm(medv ~ poly(lstat, degree = 10, raw = TRUE), data = Boston )
lm10_poly_ortho <- lm(medv ~ poly(lstat, degree = 10, raw = FALSE), data = Boston )
summary(lm10_poly)
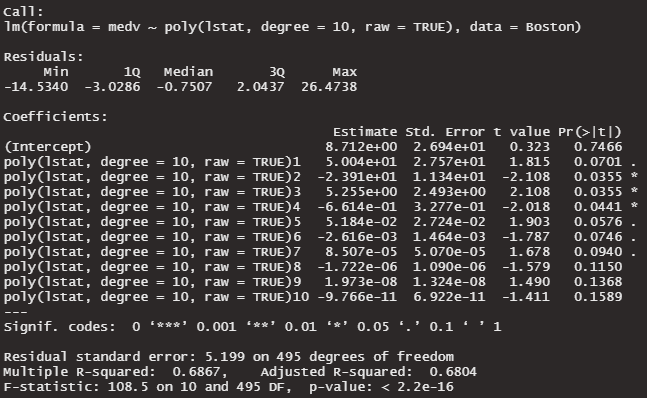
summary(lm10_poly_ortho)非直交 raw = TRUE
多くの係数が、p > 0.05になっています。係数が0である可能性を否定できません。有意水準5%で、0ではない係数は3つだけです。multicollinearityの影響でしょうか。のちに確認します。
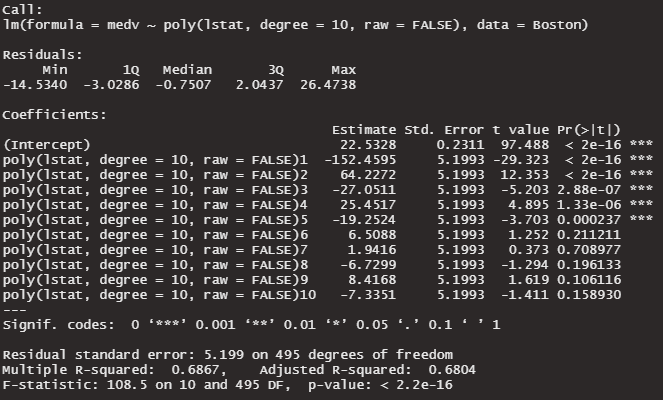
直交 raw = FALSE
有意水準5%で、0ではない係数は6つになりました。3つ多くなりました。
ところで、マルチコの検査をしてみたいと思います。
multicollinearityの診断は、VIFという指標で行います。carというパッケージで実施できます。使い方は、vif( lm( )で作ったモデル ) です。
library(car)
lm10_poly <- lm(medv ~ poly(lstat, degree = 10, raw = TRUE), data = Boston )
vif(lm10_poly)エラーがでてしまいました。
vif.default(lm10_poly) でエラー: model contains fewer than 2 terms
めんどうですが、polyを分解してdataframeを作り直す必要がありそうです。
p10 <- poly(Boston$lstat, degree = 10, raw = TRUE)
n <- cbind(medv = Boston$medv, p10)
n <- as.data.frame(n)
vif(lm(medv~. ,data=n))| 項 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| VIF | 7e+05 | 1e+08 | 6e+09 | 1e+11 | 8e+11 | 2e+12 | 4e+12 | 2e+12 | 4e+11 | 1e+10 |
VIFが5以上でダメなので、もう全部だめでmulticollinearyです。理解を深めるために、相関を見てみます。
pairs(n)
ぜんぶ相関してます。これでは、VIFが全部上がってしまうのも納得です。
今度は、Orthogonal(直交)polynonialで多項式回帰分析を実施した場合のVIFを見てみます。ちゃんとmulticollinearityの問題を排除できているでしょうか。
p10 <- poly(Boston$lstat, degree = 10, raw = FALSE)
n <- cbind(medv = Boston$medv, p10)
n <- as.data.frame(n)
summary(lm(medv~. ,data=n))
vif(lm(medv~. ,data=n))| 項 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| VIF | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
multicollinearityの問題は全くないですね。すごい。相関関係も見てみます。
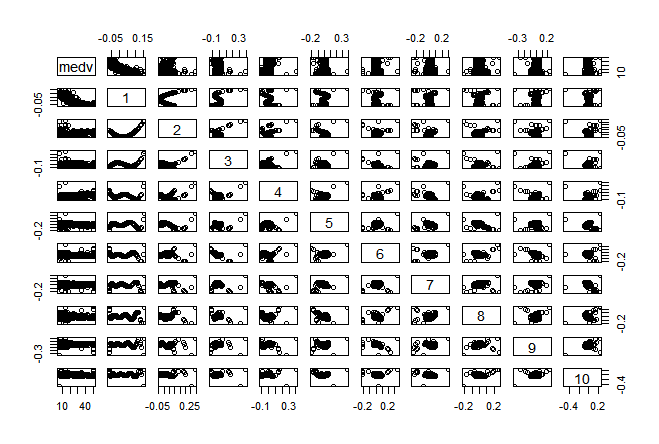
変数同士の相関がなくなってるみたいです。グラフ化してみます。
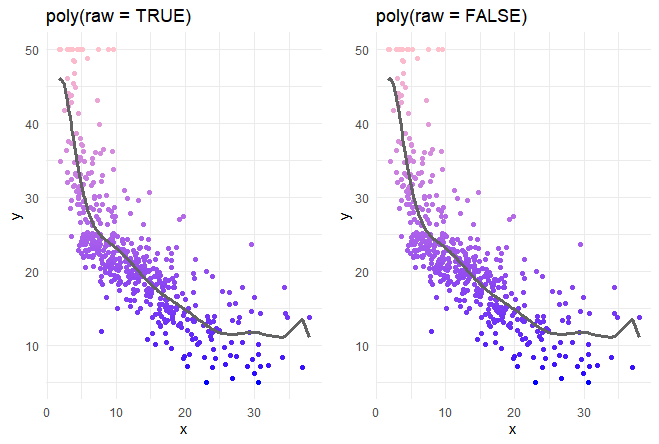
あれ、あまり変化ない感じですね。難しいことを理解したのに、効果が少なくてがっかり。
VIFの計算方法
VIFが、multicollinearityの診断をできるのはわかりましたが、どうやって計算しているのでしょうか。
VIF = 1 ÷ (1 - R^2)
R^2は、他の共変量に対する Xjの回帰における決定係数であるそうです。…..全然わからないですね。調べたところによると、以下のようになっています。
目的変数、変数1、変数2、変数3があるとする。通常通り、目的変数~変数1+変数2+変数3で回帰分析を実施する。この際、VIFがそれぞれ変数1、変数2、変数3について計算される。
変数1のVIFは、変数1を目的変数とし、変数2と変数3を説明変数とした回帰分析で算出されるR^2を使って、1 ÷ (1 - R^2)を計算した値である。つまり、変数1~変数2+変数3の回帰分析でR^2を算出すればよい。
でもどうやって?summary( lm() )したときには、Adjusted R-squaredがでてきますが、Adjustする前の数値が欲しいです。
それは、summary( lm() )$r.squareで取得できるみたいです。
さっそくVIFを計算してみたいと思います。さきほどのVIFをもう一度見てみます。
p10 <- poly(Boston$lstat, degree = 10, raw = TRUE)
n <- cbind(medv = Boston$medv, p10)
n <- as.data.frame(n)
vif(lm(medv~. ,data=n))| 項 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| VIF | 7e+05 | 1e+08 | 6e+09 | 1e+11 | 8e+11 | 2e+12 | 4e+12 | 2e+12 | 4e+11 | 1e+10 |
第1項のVIF:700000を計算してみたいと思います。第1項は、lstatの1乗です。lstatの1乗を目的変数とし、lstatの他の乗を説明変数として回帰分析を行います。そのR^2を算出し、VIF = 1 ÷ (1 - R^2)を計算します。
lmobj <- lm(lstat~
I(lstat^2)+
I(lstat^3)+
I(lstat^4)+
I(lstat^5)+
I(lstat^6)+
I(lstat^7)+
I(lstat^8)+
I(lstat^9)+
I(lstat^10),data=Boston)
summ <- summary(lmobj)
R_square <- summ$r.squared
1/(1-R_square)723961.1
小数点の計算で完全一致ではありませんが、同じになりましたね!計算方法が確認できました。
