johnsnowがコレラと水源の関係を地図にプロットして原因を突き止めたことは有名。
では、私は今の技術を使って、統計学的に有意であることを示すことはできるか。
GISはデータの種類(ポイントorポリゴン 存在orバイナリor連続値等)によって検定の手法が異なる。今のところ理解できている分類は以下。
| 分類 | 検定の名前 |
|---|---|
| ポイントデータの存在を用いた集積性の検定 | Ripley’s K/L |
| ポイントデータの連続変数を用いた集積性の検定 | Moran |
| ポリゴンの連続変数を用いた集積性の検定 | Moran, kulldorff |
Moranについてはこちら
john snowの例は、ポイントデータの存在を用いた集積性の検定となる。
今回使うライブラリはgeopandasとlibpysalとpointpats。
libpysal は PySAL(Python Spatial Analysis Library)の基盤ライブラリで、pointpats はその中の点パターン解析(Point Pattern Analysis)専用サブパッケージ”。
johnsnowのデータを取得する
import libpysal
a = libpysal.examples.available()
a
この中で、snow_mapsというのがあった。
data = libpysal.examples.load_example("snow_maps")
data.explain()
Public water pumps and Cholera deaths in London 1854 (John Snow’s Cholera Map) —————————————————————– *
以下の3つを使う。
- SohoPeople.shp: Point shapefile for Cholera deaths. (n=324)
- SohoWater.shp: Point shapefile for public water pumps. (n=13)
- Soho_Network.shp: Line shapefile for street network. (n=118)
Original data: Snow, J. (1849). On the Mode of Communication of Cholera. London: John Churchill, New Burlington Street.
コレラの死亡患者のプロットを表示
import geopandas as gpd
ppl = gpd.read_file(libpysal.examples.get_path("SohoPeople.shp"))
ppl.plot(color="red")
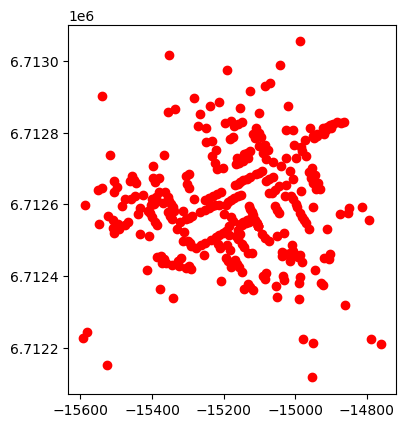
今度は水道のポンプの位置をみる
pump = gpd.read_file(libpysal.examples.get_path("SohoWater.shp"))
pump.plot(color="blue")
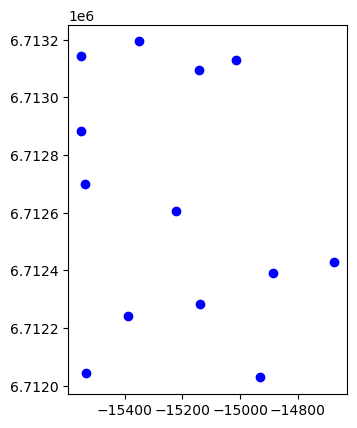
上の2つを合わせる。
import pandas as pd
ppl["category"] = "case"
pump["category"] = "pump"
df = pd.concat([ppl,pump], axis=0)
df.plot(column = "category",cmap="coolwarm_r",legend=True)
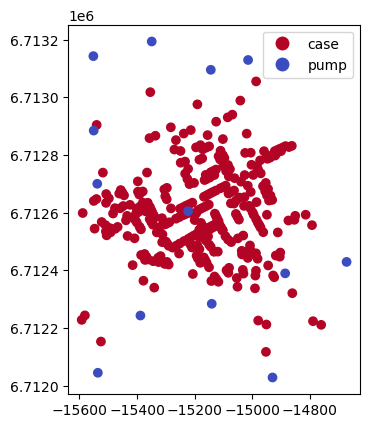
説明
pointpatsには、以下5つのripleyの関数がある。Kが多く使われているようだ。
- Ripley’s K function: 点 → 半径 d の円内に何点あるか
- Ripley’s L function: Kを線形化して解釈しやすくしたもの
- Ripley’s F function: ランダムな場所 → イベント の最近隣距離の分布
- Ripley’s G function: イベント → イベント の最近隣距離の分布
- Ripely’s J function: GとFの組み合わせ
それぞれデータから統計量が得られる。その統計量をモンテカルロ順位検定で、地域集積性の存在が否定できる可能性についてp値を出すことができる。
以下 ChatGPT
Ripley の K-test(K 関数による空間点パターンの検定)は、「点の分布がランダムか、クラスタ状か、分散(均等)か」を距離スケールごとに判定する空間統計手法です。
単一の距離ではなく「複数の距離帯で同時に」空間構造を評価できるのが最大の特徴です。
Ripley の K-test とは何か
Ripley の K 関数(K(r))を使って、観測された点パターンが 完全空間ランダム(CSR) と比べてどう違うかを調べる検定です。
何をしている検定?
– 各点のまわりに半径 r の円を描く
– その中に入る点の数を数える
– それを「ランダムに点が分布した場合の期待値」と比較する
– r を変えながら繰り返す(多スケール分析)
判定の意味
– K(r) > K_CSR(r) → r のスケールでクラスタリング
– K(r) < K_CSR(r) → r のスケールで分散(均等配置)
– K(r) ≈ K_CSR(r) → ランダム
K-test の実際の検定方法
K 関数そのものは「記述統計」ですが、Monte Carlo シミュレーションによる envelope(信頼区間) を使うことで検定として機能します。
✔ 検定の流れ
– 観測データから K(r) を計算
– CSR(完全ランダム)で多数のシミュレーションを行い、K(r) の分布を作る
– その上下限(envelope)を信頼区間とする
– 観測 K(r) が envelope を超えたら、CSR を棄却 → 有意なクラスタ or 分散
ripleyはhomoとInhomoの2つがあるが、pointpatsで実装されているのは、Homogeneousのみ。pythonで実装されたライブラリはなさそう?Rではspatstatでできるようだ。
Ripley’s Homogeneous K-function
何を仮定している?
– 点の発生強度(intensity)が 空間全体で一定 と仮定
= Complete Spatial Randomness(CSR:完全空間ランダム) を前提にする
注意点(重要)
– 背景の密度が場所によって違うデータ(都市 vs 郊外など)では、
密度の高い場所が“クラスタ”に見えてしまう誤判定が起きる
Ripley’s Inhomogeneous K-function
何を仮定している?
– 点の発生強度(intensity)が 場所によって変化すると仮定
– その変動を λ(x) として推定し、背景密度の違いを補正してから K を計算する
注意点(重要)
– λ(x) の推定(kernel bandwidth など)によって結果が大きく変わる
– 平滑化が強すぎるとクラスタが消え、弱すぎるとノイズがクラスタに見える
Ripley’s Homogeneous K-function を使うと背景の密度変動をクラスタと誤判定しやすい
例
– 都心は人口が多い
– 郊外は人口が少ない
– 事件や店舗の点データをそのまま K-test(homo)にかける
→ 都心がクラスタに見えるのは当たり前
→ しかしそれは「点の自己相関」ではなく「背景人口の密度差」
注意点
– 背景の密度が明らかに変わるデータに homo を使うと誤解釈になる
– 都市データ、環境データ、事故データなどはほぼ全部 Inhomo が必要
都市人口を考慮してもなお、空間自己相関が重要かどうかを判断するには空間自己回帰モデルを使うことも可能。pythonのspregライブラリのspreg。Rのspdepライブラリのlagsarlm()。
実行
pointpatsの関数の説明をみる。
import pointpats
help(pointpats.k_test)
Help on function k_test in module pointpats.distance_statistics: k_test(coordinates, support=None, distances=None, metric=’euclidean’, hull=None, edge_correction=None, keep_simulations=False, n_simulations=9999)
Ripley’s K function This function counts the number of pairs of points that are closer than a given distance. As d increases, K approaches the number of point pairs. When the K function is below simulated values, it suggests that the pattern is dispersed.
Parameters ———-
coordinates : geopandas object | numpy.ndarray, (n,2) input coordinates to function
support : tuple of length 1, 2, or 3, int, or numpy.ndarray tuple, encoding (stop,), (start, stop), or (start, stop, num) int, encoding number of equally-spaced intervals numpy.ndarray, used directly within numpy.histogram
distances: numpy.ndarray, (n, p) or (p,) distances from every point in a random point set of size p to some point in `coordinates`
metric: str or callable distance metric to use when building search tree
hull: bounding box, scipy.spatial.ConvexHull, shapely.geometry.Polygon the hull used to construct a random sample pattern, if distances is None
edge_correction: bool or str whether or not to conduct edge correction. Not yet implemented.
keep_simulations: bool whether or not to keep the simulation envelopes. If so, will be returned as the result’s simulations attribute
n_simulations: int how many simulations to conduct, assuming that the reference pattern has complete spatial randomness.
Returns ——- a named tuple with properties
– support, the exact distance values used to evalute the statistic
– statistic, the values of the statistic at each distance
– pvalue, the percent of simulations that were as extreme as the observed value
– simulations, the distribution of simulated statistics (shaped (n_simulations, n_support_points)) or None if keep_simulations=False (which is the default)
どれが必須のパラメーターかわからないが、チュートリアルを見ると以下の引数は入れている。
k_cluster = k_test(
coords_cluster,
hull=hull,
keep_simulations=True,
n_simulations=n_sims
)
keep_simulationsはreturnされるものを追加するパラメータで、n_simulationsはモンテカルロの回数。なので、あまり重要ではないと考えた。hullとはなんだ?教えてchatGPT
hull = 観測領域(window / study area)
pointpats の k_test は、Ripley の K 関数を使って
点パターンが CSR(完全空間ランダム)かどうかを検定する関数 です。
K 関数を計算するには、
「点がどの範囲に存在しているか」という 観測領域(window) が必須です。
この領域を pointpats では hull と呼びます。
なぜ hull が必要なのか?
K 関数では、各点を中心に半径 d の円を描き、その中の点数を数えます。
しかし、円が領域の外にはみ出すと エッジ効果(edge effect) が発生します。
そのため:
– 領域の形(矩形か、多角形か)
– 領域の境界
– 点が存在し得る範囲
を正しく指定する必要があります。
pointpats の k_test は、
hull を使ってエッジ補正(border correction)を行う ため、
領域が必須になります。
説明をよんで、疾患の観測範囲を調べる必要があると考えた。johnsnowのデータで観測範囲が分かるものを使う。
road = gpd.read_file(libpysal.examples.get_path("Soho_Network.shp"))
road.plot(color="black")
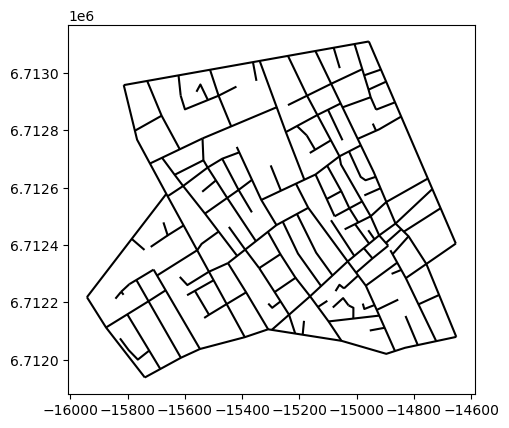
重ねて表示。
import matplotlib.pyplot as plt
fig, axe = plt.subplots(1, 1, figsize=(10, 4))
road.plot(color="black",ax=axe)
df.plot(column = "category",cmap="coolwarm_r",ax=axe)
plt.show()
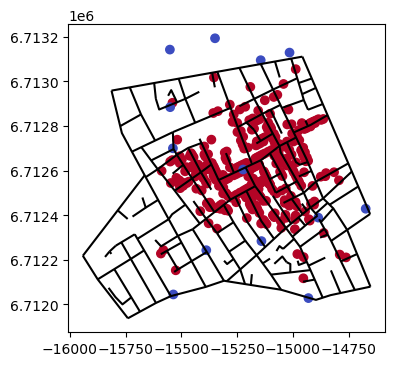
では早速実行
result = pointpats.k_test(
ppl,
hull=road,
keep_simulations=True,
n_simulations=10
)
--> 568 hull = _prepare_hull(coordinates, hull)
569 if calltype in ("F", "J"): # these require simulations
...
1581 f"The truth value of a {type(self).__name__} is ambiguous. "
1582 "Use a.empty, a.bool(), a.item(), a.any() or a.all()."
1583 )
ValueError: The truth value of a DataFrame is ambiguous. Use a.empty, a.bool(), a.item(), a.any() or a.all().
hullのところでエラーが出た模様。
hullの受け付けるタイプは bounding box, scipy.spatial.ConvexHull, shapely.geometry.Polygon
road.head()
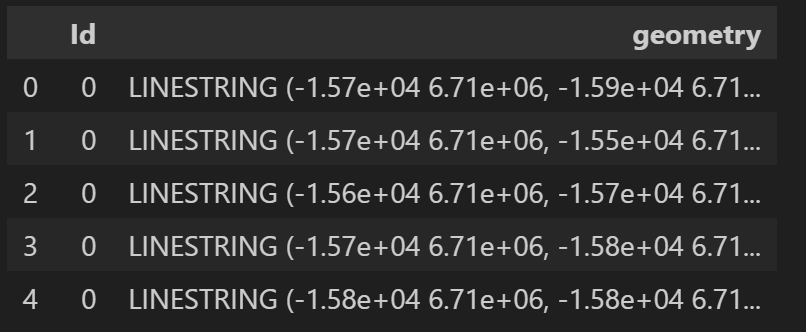
現在はLineから構成されていて、面積を求められないようだ。そのため、lineから領域に変換する。
面積を使うので、CRSを直交座標にしたい。現在のCRSを調べる。
road.crs
<Projected CRS: EPSG:3857>
Name: WGS 84 / Pseudo-Mercator
mercatorであれば直交系だが、psuedo mercatorは大体そうだが厳密ではないようだ。イギリスの直交系CRSはBritish National Grid(EPSG:27700)というのがあるようだ。
road = road.to_crs(epsg=27700)
道幅を反映させるため、bufferをつかってlineからそれぞれ5mとした(計10m)。全部を結合させる(union_all)。
buf = road.buffer(5)
studyArea = buf.union_all()
type(studyArea)
shapely.geometry.polygon.Polygon
CRS合わせてから検定をする。k_testの説明はこう書いてある。
https://pysal.org/pointpats/user-guide/ripley.html
1. Simulate many CSR patterns in the same hull.
2. Compute the statistic for each simulation.
3. Return the observed statistic, the simulated statistics, and Monte Carlo p-values at each distance.
ppl = ppl.to_crs(epsg=27700)
result = pointpats.k_test(
coordinates=ppl,
hull=studyArea,
keep_simulations=True,
n_simulations=199
)
約4分
radius = result.support # 半径
observed = result.statistic # 観測のK(r)
sims = result.simulations # モンテカルロのK(r) CSR(complete spetial Randomness)
pvals = result.pvalue # p value
radius
array([ 0. , 5.46066185, 10.92132371, 16.38198556,
21.84264742, 27.30330927, 32.76397113, 38.22463298,
43.68529484, 49.14595669, 54.60661855, 60.0672804 ,
65.52794226, 70.98860411, 76.44926597, 81.90992782,
87.37058968, 92.83125153, 98.29191339, 103.75257524])
範囲の最大の半径が103mで、デフォルトの分割数が30のようだ。そのため、5.4mごとにradiusを変えている。ちなみに、bounding boxを見ると少し不可解。なにかよしなにやっているのだろう。
x1,y1,x2,y2 = studyArea.bounds
print(x2 - x1)
print(y2 - y1)
816.361257852288
752.041637541086
x1,y1,x2,y2 = ppl.union_all().bounds
print(x2 - x1)
print(y2 - y1)
521.6952509438852
582.6630800202838
observed
array([ 0. , 115.82554555, 1291.45483291, 2606.07477492,
4134.97197621, 6098.21497332, 8298.90033881, 11090.29598661,
14350.7850939 , 17941.37700602, 21815.74150474, 25817.51410356,
30357.8754892 , 35089.34902501, 40289.9160203 , 45733.71666124,
51443.91605696, 56864.5515888 , 62522.62948902, 68609.26190778])
sims
array([[ 0. , 235.9169103 , 865.02867108, ...,
32197.041186 , 35398.77068286, 38915.05606012],
[ 0. , 318.33813325, 1064.78616985, ...,
33282.80069045, 37432.17359975, 41581.54650905],
[ 0. , 279.82294575, 1040.9413582 , ...,
34921.90362993, 38537.21608905, 42589.05234355],
...,
sims.shape
(199, 20)
pvals
array([0. , 0. , 0.005, 0.005, 0.005, 0.005, 0.005, 0.005, 0.005,
0.005, 0.005, 0.005, 0.005, 0.005, 0.005, 0.005, 0.005, 0.005,
0.005, 0.005])
p値が0.05以下なので、どれもCRSを帰無仮定にすると否定できることが分かった。つまり地域集積性あり。
可視化。
radius = result.support # 半径
observed = result.statistic # 観測のK(r)
sims = result.simulations # モンテカルロのK(r) CSR(complete spetial Randomness)
lower = sims.min(axis=0)
upper = sims.max(axis=0)
plt.figure(figsize=(7,5))
# simulation (called as envelope)
plt.fill_between(radius, lower, upper, color="lightgray", label="CSR envelope")
# 観測 K(r)
plt.plot(radius, observed, color="red", label="Observed K(r)")
plt.xlabel("Distance radius")
plt.ylabel("K(r)")
plt.legend()
plt.title("K-function with CSR envelope")
plt.show()
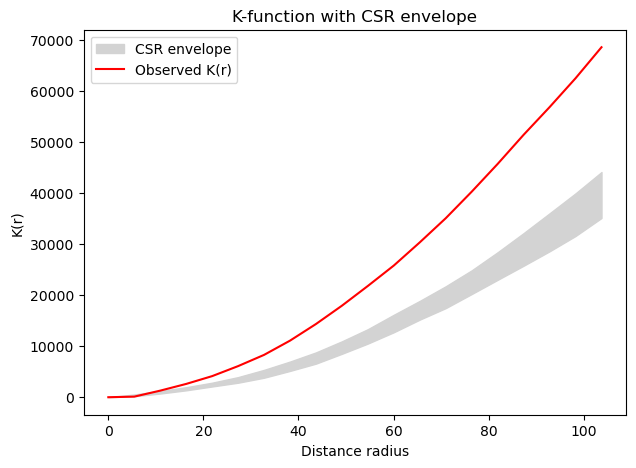
本当に検定できているのか、心配。完全にランダムなポイントの場合を検定してみる。
import numpy as np
from shapely.geometry import Point
csr_hull = np.array([0.0, 0.0, 1.0, 1.0])
csr_coords = pointpats.random.poisson(csr_hull, size=100)
points = [Point(x, y) for x, y in csr_coords]
csr_geoseries = gpd.GeoSeries(points)
csr_geoseries.plot()
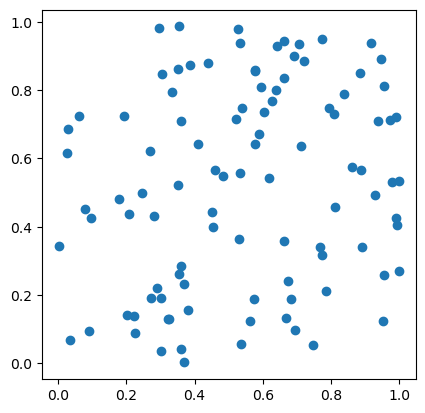
result = pointpats.k_test(
coordinates=csr_coords,
hull=csr_hull,
keep_simulations=True,
n_simulations=199
)
result.support
array([0. , 0.00713392, 0.01426783, 0.02140175, 0.02853566,
0.03566958, 0.0428035 , 0.04993741, 0.05707133, 0.06420524,
0.07133916, 0.07847308, 0.08560699, 0.09274091, 0.09987483,
0.10700874, 0.11414266, 0.12127657, 0.12841049, 0.13554441])
なぜかsupportさっきと違って20個。。さっきは30個。なぜ
result.pvalue
array([0. , 0.09 , 0.38 , 0.32 , 0.305, 0.33 , 0.425, 0.41 , 0.335,
0.39 , 0.39 , 0.395, 0.395, 0.45 , 0.345, 0.33 , 0.12 , 0.16 ,
0.135, 0.035])
radius = result.support # 半径
observed = result.statistic # 観測のK(r)
sims = result.simulations # モンテカルロのK(r) CSR(complete spetial Randomness)
lower = sims.min(axis=0)
upper = sims.max(axis=0)
plt.figure(figsize=(7,5))
# simulation (called as envelope)
plt.fill_between(radius, lower, upper, color="lightgray", label="CSR envelope")
# 観測 K(r)
plt.plot(radius, observed, color="red", label="Observed but CSR K(r)")
plt.xlabel("Distance radius")
plt.ylabel("K(r)")
plt.legend()
plt.title("K-function with CSR envelope")
plt.show()
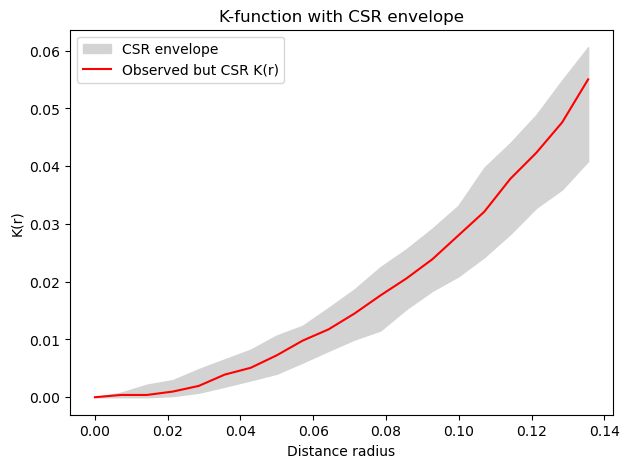
余談(今回やらない):
ある特定の地点に近づくと、り患が増えるかどうか検定する方法は、固定点における疾病の集積(forcused clustering)を検定することから、地域集積性の検定手法の中でも特にフォーカスド検定(focused clustering)と総称されている。
これはRのsplancsパッケージのDiggle-Rowlingsonの関数(tribble)を使ってできる。区域の集計データに対してはstoneの検定。こちらはRのDClusterのstone.statを使ってできる。
今回は、ポイントの集積性だけ。
補足:モンテカルロによるp値の算出
観測された統計量が、
モンテカルロで作った分布のどれくらい端にあるかを見る。
片側検定
p = ( NumberOf[monte統計量 >= 観測統計量] + 1 ) ÷ (N+1)
両側検定
p = ( NumberOf[|monte統計量 – monte統計量平均| >= |観測統計量 – monte統計量平均|)] + 1 ) ÷ (N+1)
