機械学習における変数選択の意義
機械学習において、目的変数を予想するにあたって、説明変数が必要です。説明変数が1つだと、yとxの関係なので予測が心もとないです。他の要因を考えることができません。もっと説明変数が欲しいです。
しかし逆に変数がたくさんありすぎると、必ずどこかの変数と変数が相関をもってしまうのでマルチコリナリーになって予測に悪影響を及ぼします。そこで、重要ではない変数を除き、選抜された変数で機械学習を行いたいと考えます。
変数の選択の仕方は、大きく3つあります。
- Wrapper
- Filter
- Embedding
Wrapperは、forwardとbackwardに分かれています。forwardは1づつ変数を足していっていい感じのものを見つけます。backwardは1つづつ変数を減らしていっていい感じのを見つけます。現在ではあまり使われない手法のようです。
Filterは、変数と目的変数の相関係数がある一定の数字以上のものを使う方法、1回回帰分析して変数のP値を見て不要なやつを除去する方法などさまざまなやり方があるようです。
Embeddingは、主にLASSOとRidgeが挙げられます。回帰分析はMSEを最小にするような計算が行われますが、これらは MSE + ペナルティを最小にするように計算されます。LASSOとRidegeの違いはペナルティにあります。LASSOのペナルティは、すべての係数の合計 × ペナルティの強さです。Ridgeのペナルティは、合計((すべての係数)^2) × ペナルティの強さです。Ridgeだと、2乗の効果で係数が0にならない性質があります。LASSOは、1乗の性質で係数が0になりやすいです。
ペナルティの強さはλ(ラムダ)と言います。
RidgeよりLASSOのほうが優れた結果をもたらしやすいようです(と教科書に載っていました)。というか、変数選択したいんだから係数0になってもらわないと目的を果たせないですよね。
使用するライブラリ
glmnet、データの加工にtidyverse
使うデータ
library(ISLR)の中にある野球選手の給料と成績データです。
コード
library(glmnet)
library(ISLR)
library(tidyverse)
?HittersDescription
Major League Baseball Data from the 1986 and 1987 seasons.
> colnames(playerdata)
[1] "AtBat" "Hits" "HmRun" "Runs" "RBI"
[6] "Walks" "Years" "CAtBat" "CHits" "CHmRun"
[11] "CRuns" "CRBI" "CWalks" "League" "Division"
[16] "PutOuts" "Assists" "Errors" "Salary" "NewLeague"Salaryを予測したいと思います。
train test splitを行います。
nrow(playerdata)
[1] 322
nrow(playerdata)*0.8
[1] 257.6
nrow(playerdata)*0.2
[1] 64.4
257+65
[1] 322
group_ID <- c(rep("train",length=257),
rep("test",length=65))
playerdata <- playerdata %>%
mutate(group_ID = sample(group_ID, size=322))
playerdata_train <- playerdata %>%
filter(group_ID =="train") %>%
select(-group_ID) %>%
filter(!is.na(Salary))
playerdata_test <- playerdata %>%
filter(group_ID =="test") %>%
select(-group_ID)%>%
filter(!is.na(Salary))LASSOを実施します。が、その前にデータフレームをマトリックスにしないといけません。なぜなんでしょう。。
x_matrix <- model.matrix(Salary~.,
data = playerdata_train)重要ポイント:1列目(intercept)を除きましょう!!!!なぜなら、LASSOでinteceptも変数として扱われてしまうからです。
x_matrix <- x_matrix[,-1]ようやくLASSOをフィットさせます。alpha = 1にするとLASSOで、alpha = 0にするとRidgeになります。実は、これはラムダを変えてクロスバリデーションを行っています。そのためcvがついています。そのバリデーションの結果はplotで見ることができます。
lasso <- cv.glmnet(x = x_matrix,
y = playerdata_train$Salary,
alpha = 1)
plot(lasso)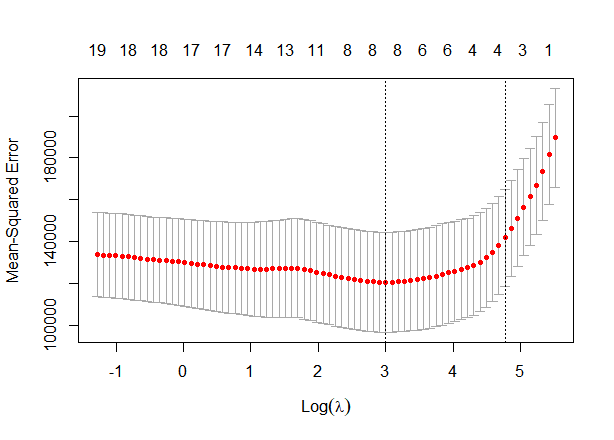
下のX軸はλをlogしたものです。e = 2.718なのでラムダが2.7を超えると1以上になります。上のX軸は変数の数です。ラムダを大きくすると変数が減ります。縦軸は、正解と予測値の誤差の大きさです。つまり、log(λ) = 3のときが誤差最小になります。点線が引いてあるところです。
でも、点線が4.8くらいのところにも引いてあるけどなんでしょう。これは、単純なモデル至上主義から来ているもので、より単純なモデルを選択しています。より単純なら変数1のほうがいいですが、それだと誤差が大きすぎる。じゃあどこならいいの?最小の誤差から1SD以内ならいい。→それが4.8くらい。という流れです。
モデルの複雑さを考えた時にモデルは複雑じゃない方が過学習しにくくなります。この1SD以内ならOKという考え方は、他でも出てきます。
ちなみに、最小のラムダの数値をしりたい場合には以下のコードで調べられます。
lasso$lambda.min
[1] 20.0517
log(lasso$lambda.min)
[1] 2.998314最小誤差から1se以内の最大ラムダを知りたい場合には、以下のコード
lasso$lambda.1se
[1] 117.4432
log(lasso$lambda.1se)
[1] 4.765955LASSOを使ってSalaryを予想するには、以下のコードです。でも、予測するのもマトリックスにする必要があることに注意です。
predict( )の変数にsがありますが、これはラムダと考えていいです。さきほど見つけた誤差が最小になるラムダを入れます。
x_test_matrix <- model.matrix(Salary~.,
data = playerdata_test)
x_test_matrix <- x_test_matrix[,-1]
pred_min <- predict(lasso,
newx = x_test_matrix,
alpha = 1,
s = lasso$lambda.min)MSE(正解との誤差)を調べます。
mean( (playerdata_test$Salary-pred_min)^2 )
[1] 74877.36ところで、もっと単純なモデルの1sd以内のlamdaを入れるとどうなるでしょう。
pred_1se <- predict(lasso,
newx = x_test_matrix,
alpha = 1,
s = lasso$lambda.1se)
mean( (playerdata_test$Salary-pred_1se)^2 )
[1] 64265.91おお!単純なモデルのほうが誤差が小さかったです!恐るべき1SD以内理論。
ところで変数の選択はどうなった?
ラムダの値を決める必要があったので、今までいろいろして来ました。
変数を見るためには、もう一度LASSOをフィットさせないといけないです。今度は、glmnetを使います。さきほどはcvが頭についていました。
lambdaは、1se以内のやつを使っています。
lasso2 <- glmnet(x = x_matrix,
y = playerdata_train$Salary,
alpha = 1,
lambda = lasso$lambda.1se)変数を見たい場合には、以下のコードです。
lasso2$beta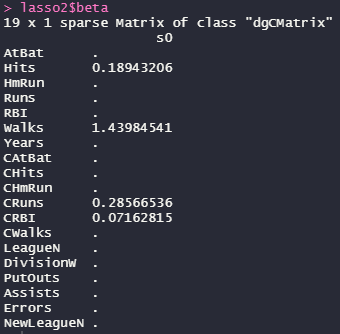
Hits、Walks、CRuns、CRBIの変数だけが選択されました!他は0に抑えられています。
教科書にあるあの図
ところで、教科書にはよくもう一つ図が載っています。実務ではあまり意味ないと思うのですが、その図も作っておきます。
さっきのglmnetのフィットにラムダを指定しないで実行します。それをプロットします。
lasso3 <- glmnet(x = x_matrix,
y = playerdata_train$Salary,
alpha = 1)
plot(lasso3)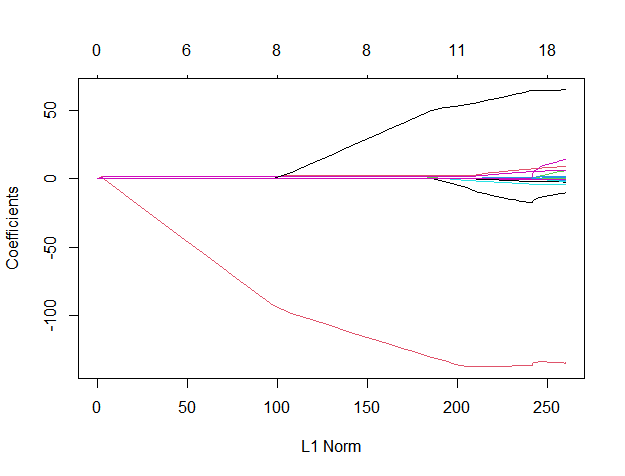
x軸の下の方のL1 Normは、係数への制限が強くなると0に近づき、制限が緩くなると大きくなります。制限が大きい方(ラムダが大きい方)が、選択される変数がすくなくなります。
x軸の上のほうは、変数の数です。
y軸は、係数です。制限を最強にすると切片だけのモデルになります。制限を緩くすると、様々な変数に対して様々な係数が大きくなっていきます。
このグラフは、勉強にはいいけどラムダの選択ができないので作る必要性はあるのでしょうか。。
