第1回:時系列解析の基礎的な関数
第2回:時系列のデータビジュアライゼーション
第3回:時系列の現状分析
第4回:時系列の予想
第5回:予想モデルの評価
使用する言語:R
パッケージ:fpp2(forecast)
前回作成した予想モデルについて、どのモデルがいいか比べてみます。いくら過去のデータの動きを模倣できても、将来の予測がうまくなければ意味がありません。
評価の方法には、train test に分けた評価、time series cross validationの2つがあります。詳しくは、時系列解析 その1を参照
time series cross validationはとても時間がかかるので、やめておきます。
train testでout of sample評価をします。
前回コロナ患者の数を様々なモデルを用いて予想しました。予想モデルを評価してどれがいいか調べてみます。(疫学的なモデル(SIRモデル)を用いて予想するのがセオリーだと思いますが、他の技術を使っています)
使用データ:厚生労働省オープンデータ(https://www.mhlw.go.jp/stf/covid-19/open-data.html)を改変
まずデータを読み込みます。2020年1月16日(土)~2021年3月22日(月)
## covid
patient <- read.csv("C:\\Users\\pcr_positive_daily.csv",encoding="UTF-8")
colnames(patient) <- c("date","pcr_positive")
patient_ts <- ts(patient$pcr_positive,start = c(1,7), frequency = 7)
autoplot(patient_ts)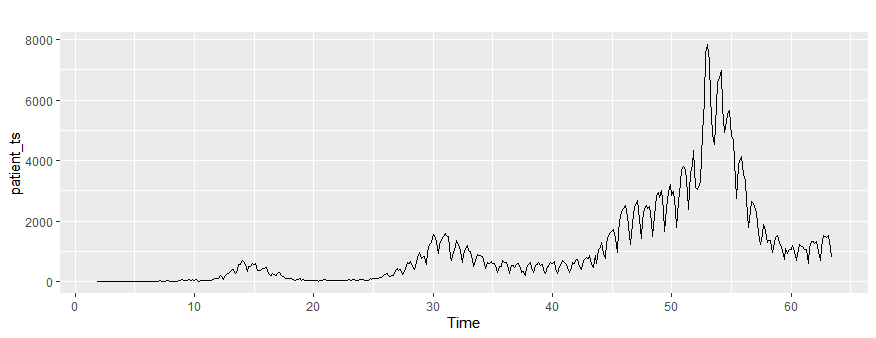
データをTrain(8割)Test(2割)に分けます。
divpoint <- round(NROW(patient_ts)*0.8)
divtime <-time(patient_ts)[divpoint]
divtime_plus1 <-time(patient_ts)[divpoint+1]
train <- window(patient_ts, end = divtime)
test <- window(patient_ts, start = divtime_plus1)それぞれのモデルをtrainデータにフィットさせます。複数の関数は、それ自体がforecastをしているので注意が必要です。
NROW(test) # 86
tslm_trend_season_fit_train = tslm(train~trend+season, data=train)
stlf_fit_train = stlf(train,method = "ets",h=86)
ets_fit_train = ets(train)
arima_fit_train = auto.arima(train)
dynamic_harmonic_regression_train = auto.arima(train, xreg = fourier(train, K = 2))
neural_network_fit_train = nnetar(train)
bagged_ets_fit_train = baggedETS(train)
bagged_arima_fit_train = baggedModel(train, bootstrapped_series = bld.mbb.bootstrap(train,3),fn=auto.arima)
tbats_fit_train = tbats(train)
mean_fit_train = meanf(train,h=86)
naive_fit_train = naive(train,h=86)
snaive_fit_train = snaive(train,h=86)
rwf_with_drift_train = rwf(train, drift = T,h=86)forecastします。上記ですでにforecastしている関数は、そのまま名前を変えているだけです。
tslm_trend_season_fit_train_forecast = forecast(tslm_trend_season_fit_train, h = 86 )
stlf_fit_train_forecast = stlf_fit_train
ets_fit_train_forecast = forecast(ets_fit_train , h = 86 )
arima_fit_train_forecast = forecast(arima_fit_train , h = 86 )
dynamic_harmonic_regression_train_forecast = forecast(dynamic_harmonic_regression_train,
h = 86,
xreg=fourier(patient_ts, K = 2, h=86))
neural_network_fit_train_forecast = forecast(neural_network_fit_train , h = 86 )
bagged_ets_fit_train_forecast = forecast(bagged_ets_fit_train , h = 86 )
bagged_arima_fit_train_forecast = forecast(bagged_arima_fit_train , h = 86 )
tbats_fit_train_forecast = forecast(tbats_fit_train , h = 86 )
mean_fit_train_forecast = mean_fit_train
naive_fit_train_forecast = naive_fit_train
snaive_fit_train_forecast = snaive_fit_train
rwf_with_drift_train_forecast = rwf_with_drift_trainAccuracyを計算します。
tslm_trend_season_eval <- accuracy(tslm_trend_season_fit_train_forecast, test)
stlf_eval <- accuracy(stlf_fit_train_forecast, test)
ets_eval<- accuracy(ets_fit_train_forecast, test)
arima_eval<- accuracy(arima_fit_train_forecast, test)
dynamic_harmonic_regression_eval<- accuracy(dynamic_harmonic_regression_train_forecast, test)
neural_network_eval<- accuracy(neural_network_fit_train_forecast, test)
bagged_ets_eval<- accuracy(bagged_ets_fit_train_forecast , test)
bagged_arima_eval<- accuracy(bagged_arima_fit_train_forecast, test)
tbats_eval<- accuracy(tbats_fit_train_forecast, test)
mean_eval<- accuracy(mean_fit_train_forecast, test)
naive_eval<- accuracy(naive_fit_train_forecast, test)
snaive_eval<- accuracy(snaive_fit_train_forecast, test)
rwf_eval<- accuracy(rwf_with_drift_train_forecast, test)データを取り出します。
n <- 9
train_eval <- data.frame(matrix(rep(NA, n), nrow=1))[numeric(0), ]
colnames(train_eval) <- c("method","ME","RMSE","MAE","MPE","MAPE","MASE","ACF1","Theil's U")
train_eval[1,1] <- "tslm_trend_season"
train_eval[2,1] <- "stlf"
train_eval[3,1] <- "ets"
train_eval[4,1] <- "arima"
train_eval[5,1] <- "dynamic_harmonic_regression"
train_eval[6,1] <- "neural_network"
train_eval[7,1] <- "bagged_ets"
train_eval[8,1] <- "bagged_arima"
train_eval[9,1] <- "tbats"
train_eval[10,1] <- "mean"
train_eval[11,1] <- "naive"
train_eval[12,1] <- "snaive"
train_eval[13,1] <- "rwf"
for(i in 1:8){
train_eval[1,i+1] <- tslm_trend_season_eval[1,i]
train_eval[2,i+1] <-stlf_eval[1,i]
train_eval[3,i+1] <-ets_eval[1,i]
train_eval[4,i+1] <-arima_eval[1,i]
train_eval[5,i+1] <-dynamic_harmonic_regression_eval[1,i]
train_eval[6,i+1] <-neural_network_eval[1,i]
train_eval[7,i+1] <-bagged_ets_eval[1,i]
train_eval[8,i+1] <-bagged_arima_eval[1,i]
train_eval[9,i+1] <-tbats_eval[1,i]
train_eval[10,i+1] <-mean_eval[1,i]
train_eval[11,i+1] <-naive_eval[1,i]
train_eval[12,i+1] <-snaive_eval[1,i]
train_eval[13,i+1] <-rwf_eval[1,i]
}
train_eval[,2:9] <- round(train_eval[,2:9], digit=1)
gridExtra::grid.arrange(gridExtra::tableGrob(train_eval))
ggplot(train_eval, aes(x=method,y=MAE, fill=MAE))+
geom_bar(stat="identity")+
scale_fill_gradient2(low="blue",mid = "skyblue", high="pink",midpoint = 150)+
coord_flip()+
theme_minimal()Train dataの結果
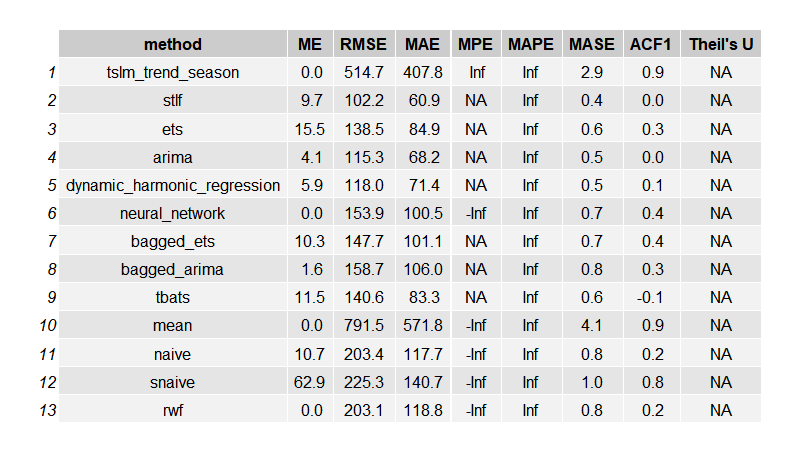
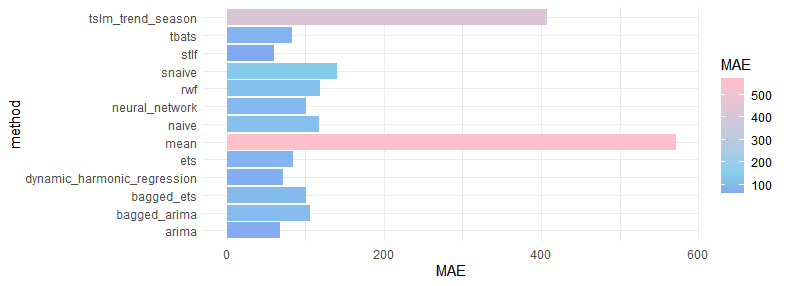
Testデータ
n <- 9
test_eval <- data.frame(matrix(rep(NA, n), nrow=1))[numeric(0), ]
colnames(test_eval) <- c("method","ME","RMSE","MAE","MPE","MAPE","MASE","ACF1","Theil's U")
test_eval[1,1] <- "tslm_trend_season"
test_eval[2,1] <- "stlf"
test_eval[3,1] <- "ets"
test_eval[4,1] <- "arima"
test_eval[5,1] <- "dynamic_harmonic_regression"
test_eval[6,1] <- "neural_network"
test_eval[7,1] <- "bagged_ets"
test_eval[8,1] <- "bagged_arima"
test_eval[9,1] <- "tbats"
test_eval[10,1] <- "mean"
test_eval[11,1] <- "naive"
test_eval[12,1] <- "snaive"
test_eval[13,1] <- "rwf"
for(i in 2:8){
test_eval[1,i+1] <- tslm_trend_season_eval[2,i]
test_eval[2,i+1] <-stlf_eval[2,i]
test_eval[3,i+1] <-ets_eval[2,i]
test_eval[4,i+1] <-arima_eval[2,i]
test_eval[5,i+1] <-dynamic_harmonic_regression_eval[2,i]
test_eval[6,i+1] <-neural_network_eval[2,i]
test_eval[7,i+1] <-bagged_ets_eval[2,i]
test_eval[8,i+1] <-bagged_arima_eval[2,i]
test_eval[9,i+1] <-tbats_eval[2,i]
test_eval[10,i+1] <-mean_eval[2,i]
test_eval[11,i+1] <-naive_eval[2,i]
test_eval[12,i+1] <-snaive_eval[2,i]
test_eval[13,i+1] <-rwf_eval[2,i]
}
test_eval[,2:9] <- round(test_eval[,2:9], digit=1)
gridExtra::grid.arrange(gridExtra::tableGrob(test_eval))
ggplot(test_eval, aes(x=method,y=MAE, fill=MAE))+
geom_bar(stat="identity")+
scale_fill_gradient2(low="blue",mid = "skyblue", high="pink",midpoint = 150)+
coord_flip()+
theme_minimal()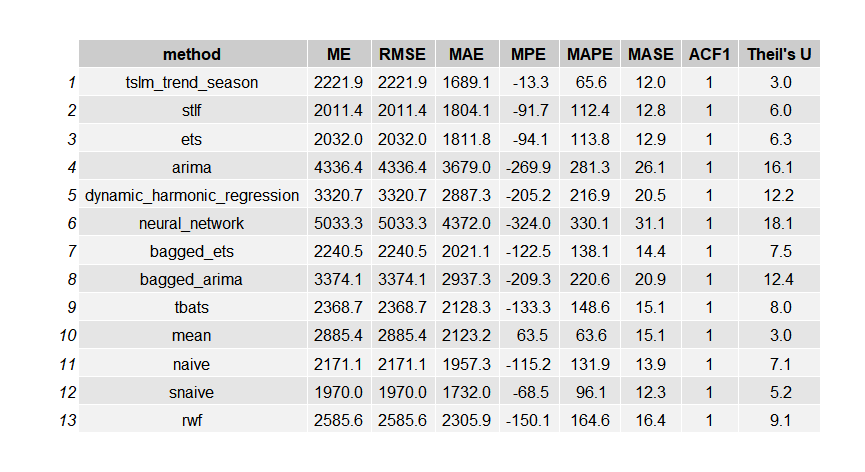
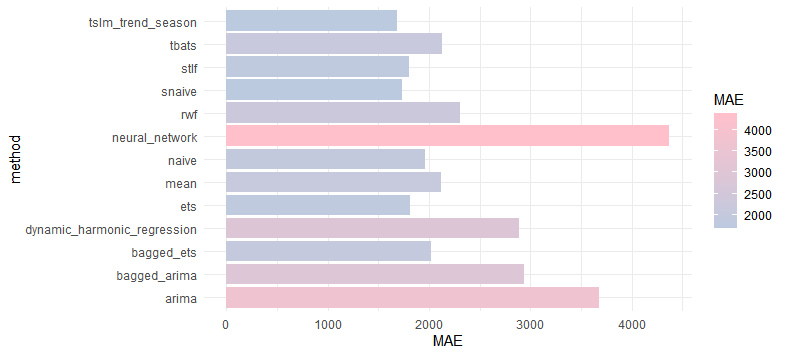
Regressionが一番いいスコアでした。
単純なseasonal naive methodがかなりいいスコア出してますね。最後の数値をただずっと予想するnaive methodがdynamic harmonic regressionを超えてたり、arimaを超えてたり。。。勉強する気なくなりますね。
特にneural network autoregressionはかなり成績が悪いですね。なんだかがっかりです。
Regressionのグラフを見てみます。
autoplot(patient_ts)+
autolayer(tslm_trend_season_fit_train_forecast$fitted)+
autolayer(tslm_trend_season_fit_train_forecast)+
theme_minimal()+theme(legend.position = "")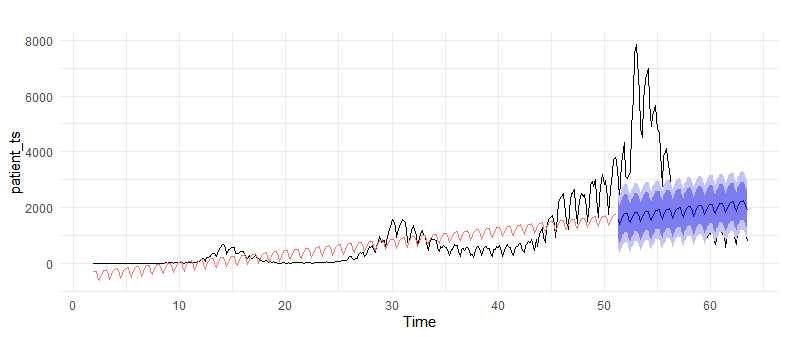
Seasonal naiveも見てみます。
autoplot(patient_ts)+
autolayer(snaive_fit_train_forecast$fitted)+
autolayer(snaive_fit_train_forecast)+
theme_minimal()+theme(legend.position = "")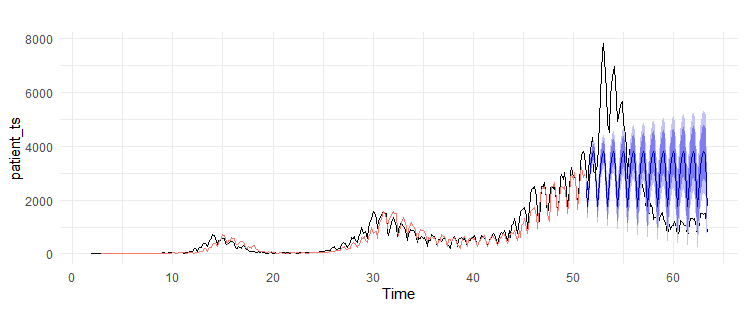
最後にneural network autoregression
Prediction Intervalを入れるために、PI=Tで計算しなおしています。
nn <- forecast(neural_network_fit_train , h = 86, PI=T)
autoplot(patient_ts)+
autolayer(nn$fitted)+
autolayer(nn)+
theme_minimal()+theme(legend.position = "")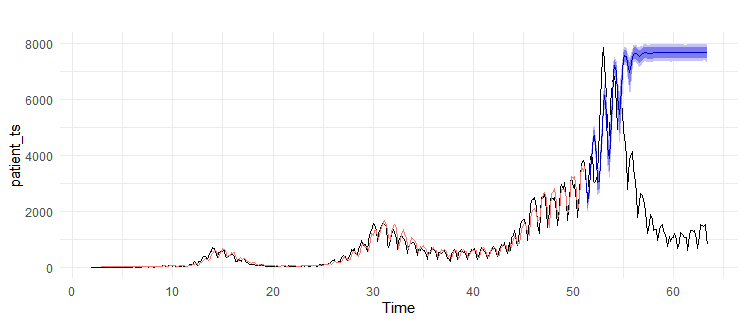
後半すごいことになっていますね!
