第1回:時系列解析の基礎的な関数
第2回:時系列のデータビジュアライゼーション
第3回:時系列の現状分析
第4回:時系列の予想
第5回:予想モデルの評価
使用する言語:R
パッケージ:fpp2(forecast)、trend
trendというパッケージの中にトレンドテストの関数が入っています。
時系列を与えられたときに時系列の分析するにはどうしたらよいでしょうか。
例えば、このグラフを見たときにこの数値は上昇傾向でしょうか。それとも下降傾向にあるのでしょうか。統計的にそれを示すにはどうしたらよいのでしょうか。
時系列データの分析は、大きく分けて3つの方法があります(と思います)。正確でないかもしれないので、自分用メモです。
1.トレンドテストを実施
2.回帰分析を実施
3.Time series decomposition
1.トレンドテスト
- Mann-Kendall Trend Test
- Pettitt’s Test for Change-Point Detection
- Pearson’s product-moment correlation
Mann-Kendall Trend Test
Mann-Kendall 検定は、時間の経過とともに一貫して増加または減少するような単調な傾向を対象としたノンパラメトリック検定です。したがって、この検定は、周期的なトレンド(濃度が交互に増加したり減少したりする)がある場合には適切ではありません。Mann-Kendall統計は、トレンドが存在するかどうか、またトレンドが正か負かを示すものです。Kendall’s Tauを計算すると、2つのデータ系列間の相関の強さを比較することができます。
例えば、完全にランダムの時系列データを作成します。これは、上昇トレンドか下降トレンドでもないはずです。
rnorm(100,mean = 5,sd=2)
random <- ts(rnorm(100,mean = 5,sd=2),frequency = 1)
autoplot(random)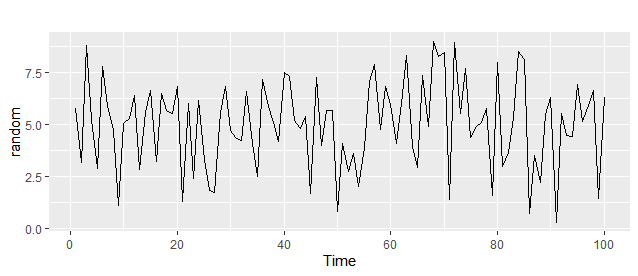
Mann-Kendall Trend Testを実施するには、trendパッケージのmk.testを使います。
mk.test(random)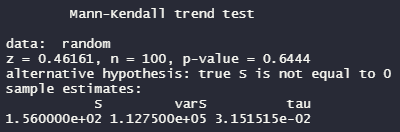
解釈:pが0.05以上だと上昇も下降もないと判断されます。
tauが+だと上昇、tauがーだと減少。
Pettitt’s Test for Change-Point Detection
時系列の傾向の変化を検定するために、Pettittのノンパラメトリック検定を行います。Pettitt’s Test for Change-Point Detectionを実施するには、trendパッケージのpettitt.test()を使います。null hypothesは変化なしです。
pettitt.test(random)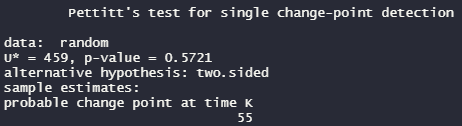
解釈:pが0.05以上だと上昇も下降もないと判断されます。時系列データ55番目のところでトレンドが変わったのかな?と、教えてくれます。
Pearson’s product-moment correlation
2つのデータ間の線形相関を表す指標。結果は常に-1から1の間の値になります。たとえば、1日目、2日目、3日目、にデータをとって結果が、45,50,60であれば(1,2,3)と(45,50,60)の相関を見ます。相関がなければ、時間とともに、上昇も下降もないと判断します。
cor.test(A,B, method=”pearson)で相関関係を見ます。time(tsオブジェクト)を使って、時間を取り出します。
cor.test(random,time(random),method = "pearson")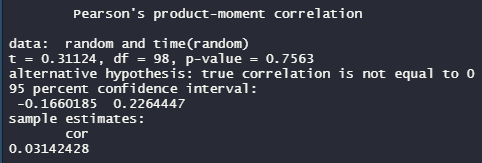
解釈: p-valueが0.05より大きい場合は、上昇下降なし(相関0の可能性高い)。pが小さいと上昇下降あり(相関あり)。
ちなみに、どのテストが一番いいのでしょうか。ランダムな数値にすこし傾向を加えてみたいと思います。以下がデータの作り方です。
時系列100のデータ = 等差数列100 + 正規分布ランダム100
例:0から1の間の等差数列100 + ランダム100
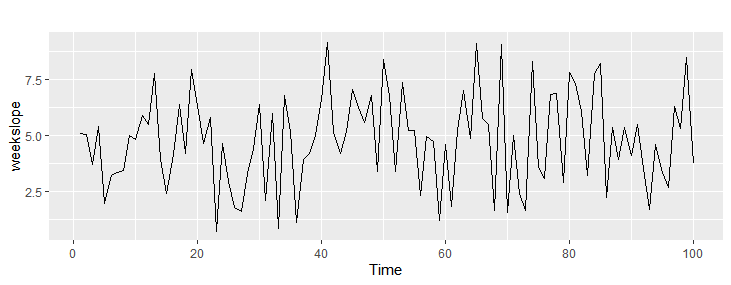
weekslope <- seq(from=0,to=1,length.out=100)+rnorm(100,mean = 5,sd=2)
weekslope <- ts(weekslope,frequency = 1)
autoplot(weekslope)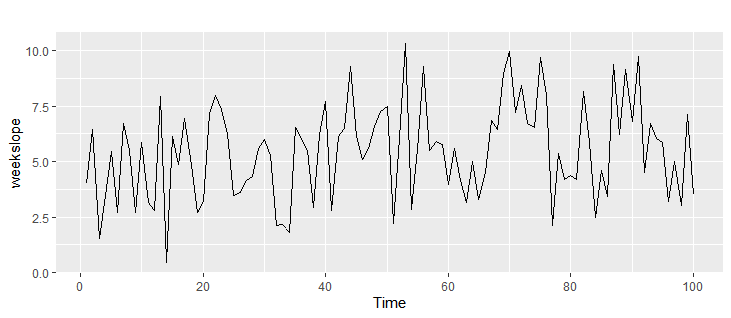
1000回のシュミレーションをしてみます。どのテストが一番、検出できたでしょうか。
# 結果をstackするデータフレームを作成
n <- 5
result_m <- data.frame(matrix(rep(NA, n), nrow=1))[numeric(0), ]
colnames(result_m) <- c("p","significant","s","vars","tau")
n <- 3
result_p <- data.frame(matrix(rep(NA, n), nrow=1))[numeric(0), ]
colnames(result_p) <- c("p","significant","U")
n <- 3
result_c <- data.frame(matrix(rep(NA, n), nrow=1))[numeric(0), ]
colnames(result_c) <- c("p","significant","cor")
# シュミレーション
for(i in 1:1000){
weekslope <- seq(from=0,to=1,length.out=100)+rnorm(100,mean = 5,sd=2)
weekslope <- ts(weekslope,frequency = 1)
mmmm <- mk.test(weekslope)
result_m[i,1] <- mmmm$p.value
result_m[i,2] <- (mmmm$p.value<0.05)
result_m[i,3] <- mmmm$estimates[1]
result_m[i,4] <- mmmm$estimates[2]
result_m[i,5] <- mmmm$estimates[3]
pppp <- pettitt.test(weekslope)
result_p[i,1] <- pppp$p.value
result_p[i,2] <- (pppp$p.value<0.05)
result_p[i,3] <- pppp$statistic
cccc <- cor.test(weekslope,time(weekslope),method = "pearson")
result_c[i,1] <-cccc$p.value
result_c[i,2] <-(cccc$p.value<0.05)
result_c[i,3] <-cccc$estimate
}
# 結果をパーセントで表示
sum(result_m$significant)/nrow(result_m)*100
sum(result_p$significant)/nrow(result_p)*100
sum(result_c$significant)/nrow(result_c)*100傾向があると判断した割合です。ちょっと傾向が弱すぎて、傾向を見つけにくかったようです。pearsonが検出率が高いようです。
| test | 傾向検出割合 |
| Mann-Kendall Trend Test | 29% |
| Pettitt’s Test for Change-Point Detection | 20% |
| Pearson’s product-moment correlation | 30% |
今度は、傾向を少し強くしてみます。
例:0から2の間の等差数列100 + ランダム100
weekslope <- seq(from=0,to=2,length.out=100)+rnorm(100,mean = 5,sd=2)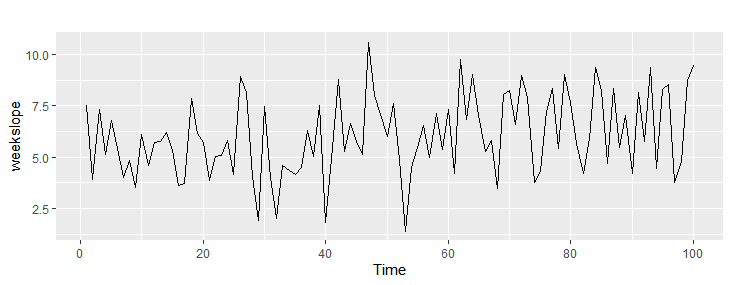
| test | 傾向検出割合 |
| Mann-Kendall Trend Test | 80% |
| Pettitt’s Test for Change-Point Detection | 68% |
| Pearson’s product-moment correlation | 81% |
また傾向を少し強くしてみます。
例:0から3の間の等差数列100 + ランダム100
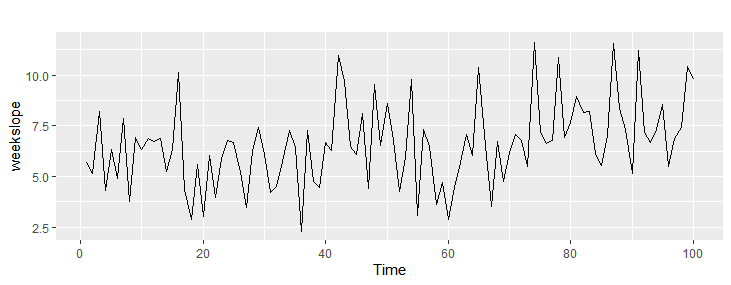
| test | 傾向検出割合 |
| Mann-Kendall Trend Test | 98% |
| Pettitt’s Test for Change-Point Detection | 96% |
| Pearson’s product-moment correlation | 99% |
こんどはランダムにします。
例:正規分布(mean = 5,sd=2)ランダム100
| test | 傾向検出割合 |
| Mann-Kendall Trend Test | 4% |
| Pettitt’s Test for Change-Point Detection | 3% |
| Pearson’s product-moment correlation | 5% |
回帰分析
回帰分析には、inferenceとpredictionの2つの機能があります。inferenceの機能を使います。
時間を説明変数にとり、数値データを目的変数にします。たとえば、1年目、2年目、3年目にデータをとり結果が10,15,20であれば、説明変数を(1,2,3)として、目的変数を(10,15,20)とします。説明変数の係数を見ることで、時間経過とともに目的変数はどう動くかを見ます。
時系列(tsオブジェクト)のregressionは、lm()ではなく、tslm()を使います。tslm()を使っておくことで、後でforecastが使えます(lmのpredictと同様)。forecastで、autolayer()でグラフを書くことができます。lm+predictだとautolayer()できません。
tslm(y~x, data)
fit <- tslm(random~time(random), data = random)
summary(fit)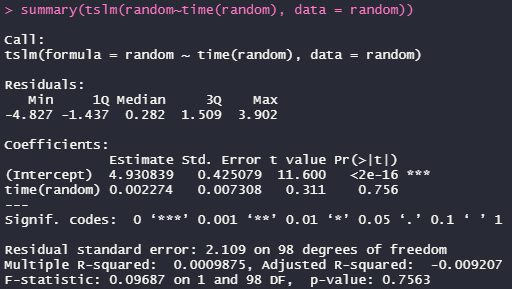
モデルのAdjusted R^2が-0.009なのでこのモデルで判断するのは危険ですが、time(random)の係数のPrが0.756なので、係数が0の可能性があります。つまり、時間とともに、上昇も下降もないということです。
ちなみに、lmでも同じ結果が得られます。
fit <- lm(random~time(random), data = random)
summary(fit)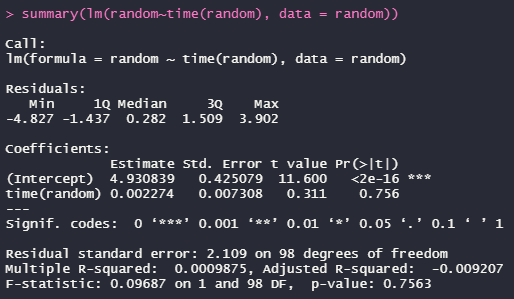
Time series decomposition
データを季節成分とトレンド成分に分解することで、時系列データの理解を深めることができます。
季節変動の大きさ、またはトレンドサイクル周辺の変動が時系列のレベルに応じて変化しない場合ある時点tでのデータは、以下のように書くことができます。
Additive decomposition : yt=St+Tt+Rt
ytはデータ。Stは季節成分。Ttはトレンド・サイクル成分,そしてRtはresidual。
季節変動やトレンドサイクル周辺の変動が時系列のレベルに比例しているような場合には、以下のように書くことができます。
Multiplicative decomposition : yt=St×Tt×Rt
ちなみに、logを使うと行ったり来たりできます。
yt=St×Tt×Rt は logyt=logSt+logTt+logRt と同じです。
Additive decomposition古典的なやり方(理解しやすい)
- トレンド・サイクルから計算します。計算は、移動平均です。tsオブジェクトのfrequencyに合わせて移動平均に組み込む数を変化させます。frequency = 7の週データなら13データを使って平均します。両端だけ、影響力を0.5にします。現在から遠いところの影響力を弱めるためです。
- 次は季節成分を計算します。データからトレンド・サイクルを引きます。その残った数値について、毎年同じ月の平均を取ります。そして、毎年上昇したり毎年下降しないように、各月の合計が0になるように調整します。具体的には、全ての月の平均から、各月の平均を引きます。
- 最後にresidualを計算します。ytから、トレンド・サイクルと季節成分を引いた値です。
Multiplicative decomposition古典的なやり方(理解しやすい)
- トレンド・サイクルはAdditive decompositionと同じ方法。
- 季節成分のところを、引くを割るにする。
- residualも、引くから割るにする。
古典的Additive decomposition使い方
decompose(tsオブジェクト,type=”additive”)
autoplot(decompose(elec,type="additive"))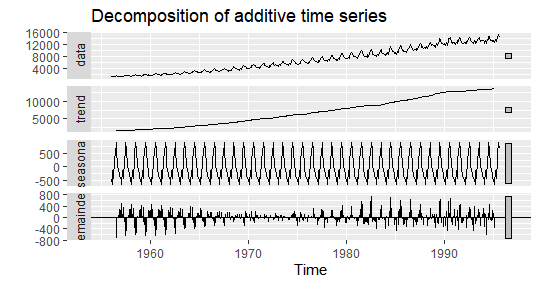
古典的 Multiplicative decompositionの使い方
decompose(tsオブジェクト,type=”multiplicative”)
autoplot(decompose(elec,type="multiplicative"))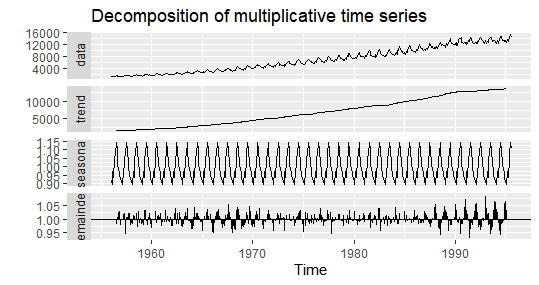
STL:推奨されるdecomposionの方法
STLは、時系列を分解するための汎用的な手法です。STLは「Seasonal and Trend decomposition using Loess」の頭文字をとったものです。loessは、locally weighted scatter plot smoothで、local regressionと言われる局所的なregeressionを次々に作成し、点推定をつなげていく方法です。
また、boxcox-transformationを実施して定常状態に持っていってからの計算をして、元に戻しているようです。
使い方
stl(stオブジェクト, s.window = “periodic”)
s.windowは、 “periodic “または季節抽出のためのラグ数。ラグ数は、奇数で少なくとも7以上。
autoplot(stl(elec,s.window = "periodic"))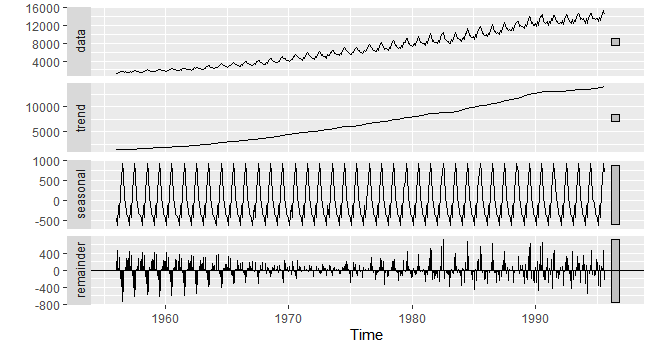
もう全部自動でお願いしますの場合は、mstlを使います。s.window=13がデフォルト。
autoplot(mstl(elec))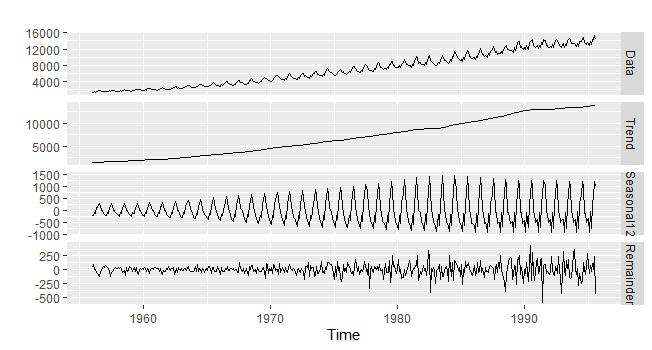
補足
関数の中身の計算を見たいときは以下の関数を実行する。
getAnywhere(関数名)
