初めに
SIRモデルとは、感染数理モデルの基礎となっているものです。感染数理モデルは難しいです。わかったと思っても、だいたいわかってないことが多いです。なにを目的に計算をしているのか、そこを見失いがちです。
私の理解では、SIRモデルは感染者を予測するためのモデルではなく、本物の感染数の動態に近くなるようなモデルを作成して、そのときのbeta、gamma、R0といったパラメータを求めることによって感染状況を把握しやすくするためです。betaは感染率と呼ばれる定数であり、各感染者が1日に病気を広める平均人数です。gammaは1日あたりに病気から回復する率です。R0の定義は、全員が感受性の集団の1人が感染した場合、その1人が新しく何人に感染させるか、その感染者の平均数を指します。
これらのパラメータがわかることで以下の重要な指標がわかります。
感染期間 ≒ 1/gamma
R0 = beta * 人口/ gamma SIRを人数で計算した場合
(R0 = beta / gamma SIRを割合で計算した場合)
感染を抑えるためワクチンを打たなければいけない割合 = 1-1 / R0
今回は、第3波のときの感染数からSIRモデルを使ってコロナのR0基本再生産数を計算したいと思います。R0の定義は、全員が感受性の集団の1人が感染した場合、その1人が新しく何人に感染させるか、その感染者の平均数を指します。そのため、定義からいうと感受性集団である場合にしかR0は計算できなくなり、つまり第1波でしか計算できないということになります。でも、第3波のときには変異株もでてきたことだし、全体に比べて免疫をもった人は1%にも満たないので、とにかく計算してみます。
データ
東京都のサイトからデータを取ってきます。日にちごとの感染者数が載っていませんので加工するひと手間があります。以前の記事で、加工の方法を記載しました。
東京都サイト:https://catalog.data.metro.tokyo.lg.jp/dataset/t000010d0000000068/resource/c2d997db-1450-43fa-8037-ebb11ec28d4c
上記の加工を終えて、2020年1月24日から2021年6月23日までの日ごとの感染者数のCSVができあがりました。
df <- read.csv("covid-tokyo.csv")
head(df)date number 1 2020-01-24 1 2 2020-01-25 1 3 2020-01-26 1 4 2020-01-27 1 5 2020-01-28 1 6 2020-01-29 1
今回は、第3波のところだけ(2021-03-04~2021-06-10)を使うので、日にちでスライスします。
df <- read.csv("covid-tokyo.csv")
df$date <- as.Date(df$date,fomat="%Y-%m-%d")
df_3rd <- df %>% filter(date >= "2021-03-04" & date <= "2021-06-10")
ggplot(df_3rd)+
geom_line(aes(x=date,y=number,color="True"))+
scale_x_date(date_breaks ="7 day")+
theme(axis.text.x = element_text(angle = 90))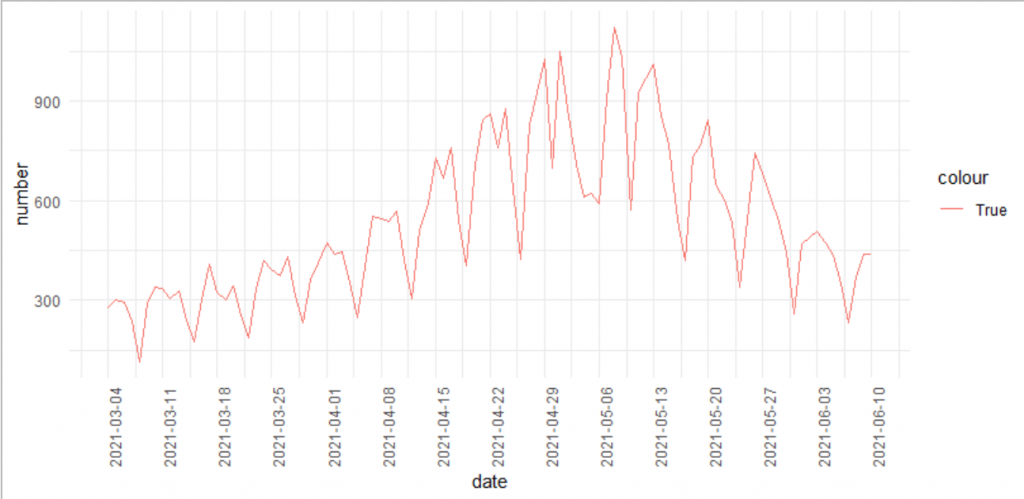
SIRモデルから S:感受性の人数 I:感染者数 R:免疫を有する人数 を求めるには、以下の微分方程式を解く必要があります。微分方程式をとくにはdeSolveというパッケージを使います。
dS <- -beta * I * S
dI <- beta * I * S - gamma * I
dR <- gamma * I以下の関数は公式だとおもってコピペした方がよさそうです。
sir_1 <- function(beta, gamma, S0, I0, R0, times) {
require(deSolve) # for the "ode" function
sir_equations <- function(time, variables, parameters) {
with(as.list(c(variables, parameters)), {
dS <- -beta * I * S
dI <- beta * I * S - gamma * I
dR <- gamma * I
return(list(c(dS, dI, dR)))
})
}
parameters_values <- c(beta = beta, gamma = gamma)
initial_values <- c(S = S0, I = I0, R = R0)
out <- ode(initial_values, times, sir_equations, parameters_values)
as.data.frame(out)
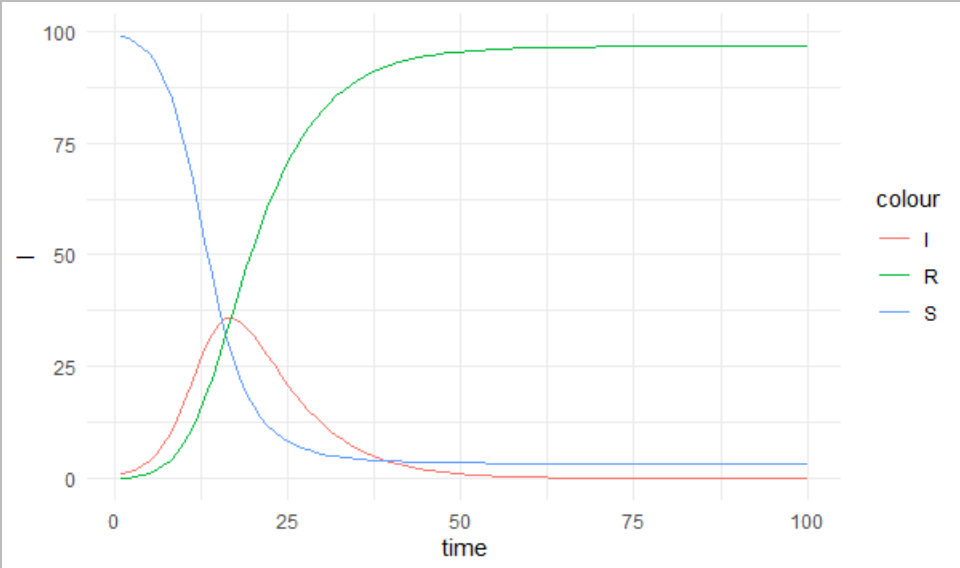
}上記の関数を使ってSIRモデルを解くと、S、I、Rについて、時点ごとに人数が計算できます。適当にbeta、gammaとか入れて、グラフにしてみます。
prediction <- sir_1(beta = 0.005, # infectious contact rate (/person/day)
gamma = 1/7, # recovery rate (/day)
S0 = 99,
I0 = 1,
R0 = 0,
times = 1:100)
ggplot()+
geom_line(data=prediction, aes(x=time,y=I,color="I"))+
geom_line(data=prediction, aes(x=time,y=S,color="S"))+
geom_line(data=prediction, aes(x=time,y=R,color="R"))+
theme_minimal()
よく見る図が描けました。でも、これってパラメータを適当に入れたので何の意味もない図です。
今度は、数字をいろいろ試して実際の第3波のグラフの形に、Iの線(赤色)を近づけていきたいと思います。S0、I0、R0(resistanceの方)は、東京都の人口、第3波入口の日にちの感染者数、入口までに感染した人の数を使って計算して入れます。gammaは、感染期間 ≒ 1/gammaの関係を使って、感染期間を7日と予想して適当に入れています。betaも適当に入れています。最初は、驚くほど実際の感染者数のグラフと異なるので、パラメータを試行錯誤しながら近づけていきます。
prediction <- sir_1(beta = 0.0000000113, # infectious contact rate (/person/day)
gamma = 1/7, # recovery rate (/day) 7日で回復するとして1/7
S0 = (13960236 - 279 - 112394), # 東京の人口 13960236
I0 = 279, # 2021-3-4の感染者数
R0 = 112394, # 2021-3-3までの感染者数
times = 1:length(df_3rd$date))
ggplot()+
geom_line(data=df_3rd,aes(x= 1:length(date),y=number,color="True"))+
geom_line(data=prediction, aes(x=time,y=I,color="Prediction"))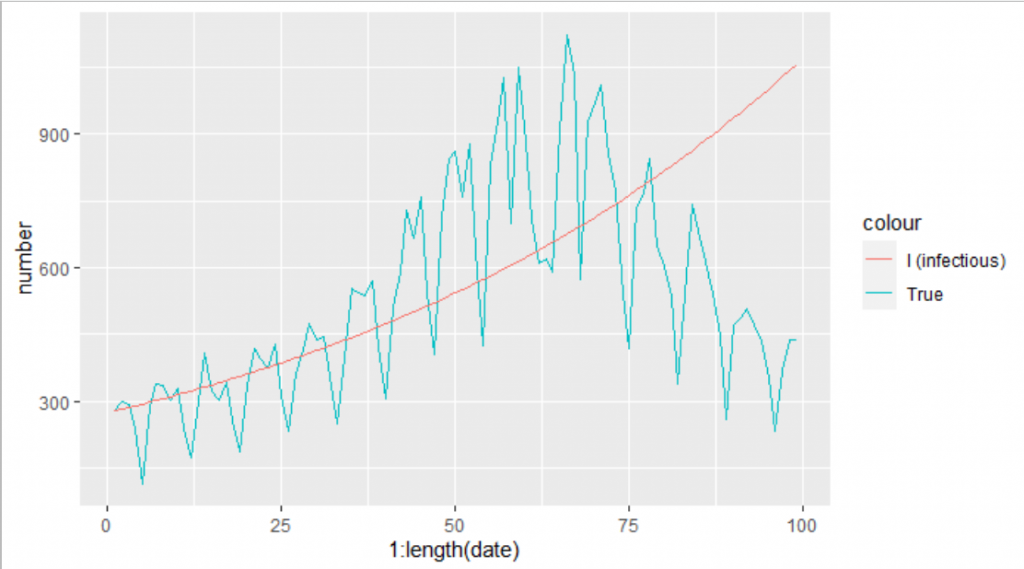
近づいてきました。が、しかしこんなに適当にパラメータを決めていいのでしょうか。いやダメです。一番、実際のモデルと近くなるようなパラメータを探さないといけないのです。
ではどこを目指してパラメータを動かせばいいでしょうか。実際の値とSIRモデルのIの値の差が、小さくなるところを目指します。差がマイナスになるのが嫌なので、2乗してからその合計を指標とします。この指標を最小にするパラメータのbetaとgammaの組み合わせ探します。
例えば、今の状況だとどれくらいの指標の値となるのでしょうか。
sum ((prediction$I - df_3rd$number)^2)7039947
この値をさらに小さくしたいです。Rにはoptimという関数があって、optim(パラメータ初期値、計算方法)を実行すると、計算が生み出す値を、最小にするパラメータを見つけてくれます。
ss <- function(input) {
predictions <- sir_1(beta = input[1],
gamma = input[2],
S0 = (13960236 - 279 - 112394),
I0 = 279,
R0 = 112394,
times = 1:length(df_3rd$date))
sum((predictions$I - df_3rd$number)^2) # -1は最初の値を抜いている。
}
starting_param_val <- c(0.0000000113, 1/7)
ss_optim <- optim(starting_param_val, ss)
ss_optim$par [1] 1.131786e-08 1.464268e-01 $value [1] 5167730
さきほどの値(7039947)よりも指標が小さくなるbetaとgammaの組み合わせを見つけることができました。
さっそくこれらの数値をつかって、再度グラフを書いてみます。
prediction <- sir_1(beta = 1.131786e-08, # infectious contact rate (/person/day)
gamma = 1.464268e-01, # recovery rate (/day) 7日で回復するとして1/7
S0 = (13960236 - 279 - 112394), # 東京の人口 13960236
I0 = 279, # 2021-3-4の感染者数
R0 = 112394, # 2021-3-3までの感染者数
times = 1:length(df_3rd$date))
ggplot()+
geom_line(data=df_3rd,aes(x= 1:length(date),y=number,color="True"))+
geom_line(data=prediction, aes(x=time,y=I,color="Prediction"))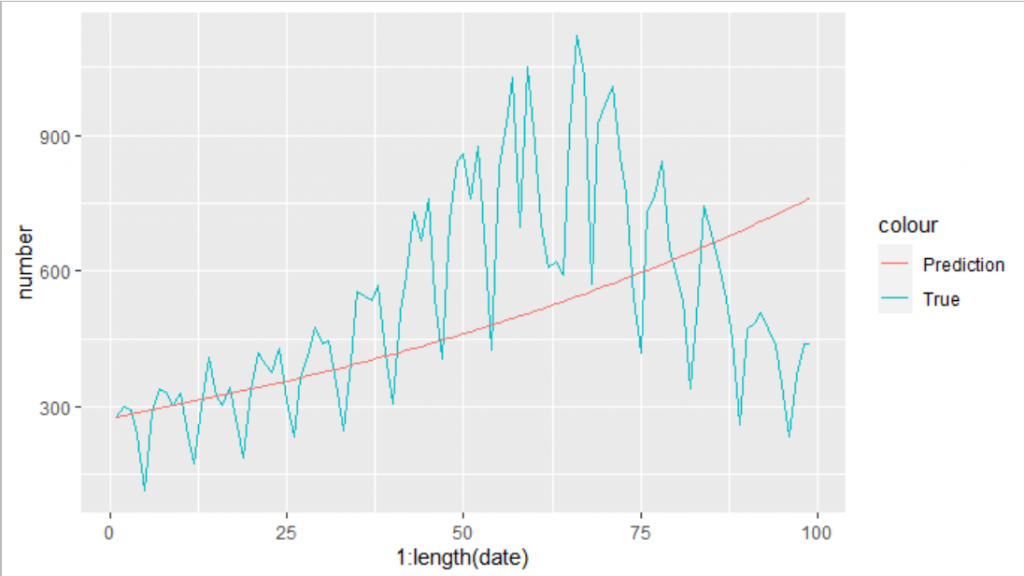
できました。これでgammaとbetaの値を求めることができました。それではお待ちかねのR0の計算を行います。今回は、SIRに実数をつかったのでR0の計算は、R0 = beta * 人口/ gamma です。
(13960236) * 0.00000001131786 / 0.14642681.079037
R0はだいたい1となりました。感染収束してきたのだから、当たり前でしょうか。やはり私は、SIRモデルをやっているとなにを目的に計算をしているのか、見失ってしまいます。
