時系列解析についてまとめたいと思います。
第1回:時系列解析の基礎的な関数
第2回:時系列のデータビジュアライゼーション
第3回:時系列の現状分析
第4回:時系列の予想
第5回:予想モデルの評価
使用する言語:R
パッケージ:fpp2(forecast)
パッケージについて
fpp2パッケージは、forecastパッケージと時系列のサンプルデータを含んだ総合パッケージです。tidyverse的な立ち位置です。
forecastは、fableの古いバージョンです。fableパッケージは、tidyverseとの連携が強化されています。ただ、2019年から開発されているtableパッケージは発展途上です。forecastパッケージは2009年から開発されているので、完成度が高いです。どちらを今から学ぶか悩ましいですが私は、forecastパッケージを学ぶという選択をしました。
tsオブジェクトの使い方
tsオブジェクト(time series object)とは、時系列解析に特化したオブジェクトです。forecastパッケージは、tsオブジェクトを要求します。
使い方は、ts ( start = … , end = … , frequency = … ) です。
startの使い方。始まりの時を指定します。
values <- c(3,4,5,6,7)
tsvalues <- ts(values, start = 1990, frequency = 1)
# 1990年、1991年、1992年、1993年、1994年endの使い方。終わりの時を指定します。
values <- c(3,4,5,6,7)
tsvalues <- ts(values, end = 1990, frequency = 1)
# 1986年、1987年、1988年、1989年、1990年frequencyの使い方。 周期を指定します。1年1個のデータなら、1。1年4回のデータなら、4。1年12個のデータなら12です。
4半期データの場合
values <- c(3,4,5,6,7)
tsvalues <- ts(values, start = 1990, frequency = 4)
# 1990年 Qtr1 Qtr2 Qtr3 Qtr4、 1991年 Qtr1 月ごとのデータの場合。start = c (A,B)と指定します。Aは年。Bは周期のナンバリングです。以下の場合は月ごとのデータなので、B=4とすると4月となります。
values <- c(3,4,5,6,7)
tsvalues <- ts(values, start = c(1990,4), frequency = 12)
# 1990年 Apr May Jun Jul Aug日ごとのデータは特殊です。2種類のfrequencyの指定の仕方があります。解析に合わせて選びます。わからない場合は、数年を超えるデータがある場合はタイプ1、2年以内であればタイプ2がいいのではないかと思います(個人的な意見)。
タイプ1 1年単位で指定 frequency = 365 もしくは365.25
タイプ2 1週間単位で指定 メリット:曜日ごとのseasonplotができます。
values <- c(3,4,5,6,7)
# タイプ1 1年単位
anl <- ts(value, start = c(2021,1), frequency =365)
# タイプ2 1週間単位 → seasonplotできる
anl <- ts(value, start = c(1,6), frequency =7) タイプ2のc(1,6) :1は第〇週で、6は、日、月、火、水、木、金の金を指す。
windowの使い方
windowは、時間を用いたスライスです。このように使います。
window(tsオブジェクト, start = 1990, end = 1995)
例えばfrequency = 7のデータで、〇曜日だけ取り出したいということもできます。
myts <- ts(data, start = c(1,1), frequency = 7)
monday <- window(myts,start = c(1,2),frequency=1)
tuesday <- window(myts,start = c(1,3),frequency=1)Train(8割)、Test(2割)スプリットのやり方です。
divpoint <- round(NROW(elec)*0.8)
divtime <-time(elec)[divpoint]
divtime_plus1 <-time(elec)[divpoint+1]
train <- window(elec, end = divtime)
test <- window(elec, start = divtime_plus1)Lagged predictors
広告のように投資した時間より後に、売り上げに効果が表れる要素があります。そういった場合には過去データを使用して売り上げを予想すると精度がいいです。その変数がlagged predictorです。dynamic regression等に使用されます。その作り方を説明します。
tsオブジェクトの場合
stats::lag(データ, k=1)
kはラグ数です。
data frameの場合
mytsobject$diff <- c(NA, base::diff(mytsobject$variable1, lag = 1))
lag数を数字で指定します。diffという名前のついた列を追加してそこにvariable1のラグを代入します。
tscleanの使い方
時系列データには、欠損値・外れ値がありがちです。これらは、予測の精度を下げてしまいます。tsclean()で自動で修正してくれます。
tsclean()
欠損値と外れ値を別々に修正したい場合。
na.interp() # 欠損値補完
非季節性系列に対して線形補間。季節性系列の場合は、STL分解。
tsoutliers() # 外れ値補正
非季節性系列ではa running lines smootherを、季節性系列では周期的stl分解で外れ値を特定し補完。
定常状態にする系(Stationarity trend)
定常状態じゃないと、使えないモデルがあるので変形させる機能が用意されています。autoでやってくれる関数が多いので、個別の必要性はいまいちわかりません。lambdaで変形の強さを決めます。最適なlamdaを見つける機能は、autoの予測関数にlambdaを入れる際にかなり使えます。
Box-Cox transformations
BoxCox(データ, lambda = 1)
Box-Cox transformationsの最適ラムダを見つける:これはハイパーパラメータの推定に使えます。
BoxCox.lambda(データ)
Differencing
例えば、感染者の合計数のデータがある際に、前日と当日の差を引くことで1日あたりの感染者数がでてきます。合計数のデータは、右に上昇していく傾向を持ち定常状態じゃないですが、感染者数は定常状態に近くなります。(例えが良くなかったです)
diff(データ, lag = 数字) # 数字はラグ数
定常状態にさせるために最適なラグ数を調べる方法
ndiffs(データ) →結果1はlag = 1
nsdiffs(データ)→結果1はlag = 12
予測モデルを評価する系
時系列でも、通常の機械学習と同様にtest、trainにデータセットを分けてモデルを評価します。それに加えて、residualの自己相関・歪みのチェックも必要になります。自己相関のチェックから解説します。
Checkresiduals
予測値と実測値の差(Residuals)が、自己相関がないか・ゆがんでいないかをチェックします。
自己相関とは、過去のデータと相関があることです。もし、現在の数値に過去の影響が強い場合は自己相関が強く出ます。
residualsの自己相関の話をします。residualsは、予測値と実測値の差なので予測がうまくいけば0です。現実的に0は不可能ですが、実測値のパターンをうまく真似できれば、residualsは0を平均とした正規分布をします。そのresidualsに自己相関がある場合は、予測モデルはパターンを模倣できていないのでに情報取り残しがあり、良くないモデルです。まだ、モデルを改善できるはずです。
また、residualsは正規分布するのが理想ですが、どちらかに偏っていたら予想がうまくいっていません。モデルで数値を予測した際には、Prediction intervalは正規分布すると仮定して算出されます。そのため、residualsが歪んでいると算出されたprediction intervalsが不正確になります。residualが偏っていたら、他の方法でprediction intervalを計算します。
使い方は、以下です。予想したオブジェクトを入れ込みます。
checkresiduals(モデル)
関数を実行すると最後に、residualの自己相関をチェックするLjung-Box test(regressionは、Breusch-Godfrey test)が実行されます。
例:etsを使って予測したときのresidualを見る場合
checkresiduals(ets(データ))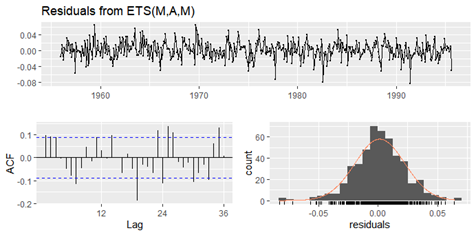
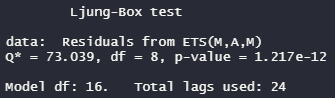
解釈:p-valueが0.05以下だと自己相関あり。モデルに情報取り残しがあり、良くないモデル。0.05以上だと、自己相関ないのでよいモデル。
例:regressionを使って予測したときのresidualを見る場合
checkresiduals(tslm(elec~season+trend))
accuracyの使い方
他の機械学習と同様、train、testのデータセットに分けてモデルの評価をします。以下のように、時系列のある時点を境にtrainとtestに分けます。trainだけを学習させて、test分の期間を予測します。その予測と実測値を比べてモデルの評価をします。

accuracy()は、以下の評価指標を算出します。
accuracy (モデル)で、trainと予測の評価
accuracy(モデル, test)で、testと予測の評価
- ME: Mean Error
- RMSE: Root Mean Squared Error
- MAE: Mean Absolute Error
- MPE: Mean Percentage Error
- MAPE: Mean Absolute Percentage Error
- MASE: Mean Absolute Scaled Error
- ACF1: Autocorrelation of errors at lag 1.
例:etsで予測したものを評価
train <- EuStockMarkets[1:200, 1]
test <- EuStockMarkets[201:300, 1]
fit1 <- forecast(ets(train),h=100)
accuracy(fit1)
test setでの評価
accuracy(fit1, test)tsCVの使い方
これはcross validationを行う関数です。time seriesでのcross validationは以下のような概念で実施します。
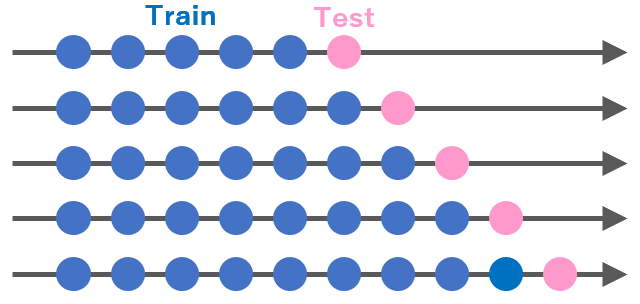
これは、非常に計算に時間がかかります。tsCV()を実施すると、time series以外の機械学習のときの感覚より数倍以上かかります。基本的な使い方は、以下です。
e <- tsCV(elec,forecastfunction=予測関数,h=10)
mse <- colMeans(e^2, na.rm = T)
RMSE <- sqrt(mean(e^2, na.rm=TRUE))
使い方は少し癖があります。
癖1:forecastfunctionに指定できる関数が不明確です。splinefとかは指定できましたが、auto.arimaとかは自作関数を作らないといけません。自作関数は、xとhの変数を受け取るように作ります。以下に例を付けます。
癖2:tsCVの返り値は、実測値と予測値の差のベクトルです。そのため、評価指標にするために一工夫が必要になります。
myfunc <- function(x, h){forecast(auto.arima(x),h=h)}
e <- tsCV(elec,forecastfunction=myfunc,h=10)
mse <- colMeans(e^2, na.rm = T)
RMSE <- sqrt(mean(e^2, na.rm=TRUE))上記の例だと、auto.arima自体が複数のモデルの中から最適なモデルを選抜するというアルゴリズムを持っているので、毎回のクロスバリデーションの試行毎に新たなモデルが作成されてしまうので、よくないかもしれません。auto系(stlf,ets,auto.arima等)には注意です。
